Uma condições suficiente de diferenciabilidade para várias variáveis
De uma perspectiva gráfica, quando uma derivada de uma função de uma variável é contínua num ponto, podemos seguramente afirmar que a função é diferenciável ali. Esta é a forma matemática de se definir a "suavidade" de uma função. O mesmo conceito pode ser estendido à funções de várias variáveis. Se as derivadas parciais forem contínuas, a função é diferenciável. Este teorema é um atalho, uma ferramenta, para ser usado quando queremos saber se uma função é diferenciável sem recorrer à definição.
Alguém pode ter perguntado sobre a derivada direcional. Lembre-se que a derivada direcional acha uma taxa de variação numa certa direção, não uma função. Não faz sentido estudar a continuidade de um valor. Estudamos a continuidade de uma função.
Cuidado com alguns pressupostos aqui! De um teorema anterior sabemos que ser diferenciável implica em ser contínua, porque uma função descontínua não pode ser diferenciável. Porém, algumas funções contínuas falham em serem diferenciáveis. Mais ainda, as derivadas parciais por si só não são suficientes para provar que uma função é diferenciável. O fato de uma função ser diferenciável não implica que as derivadas parciais sejam contínuas! A função precisa ser contínua para ser diferenciável, mas as derivadas por si mesmas podem ser descontínuas.
Seja [math]\displaystyle{ f }[/math] uma função com derivadas parciais contínuas num domínio aberto [math]\displaystyle{ D }[/math]. Então [math]\displaystyle{ f }[/math] é diferenciável em todos os pontos de [math]\displaystyle{ D }[/math].
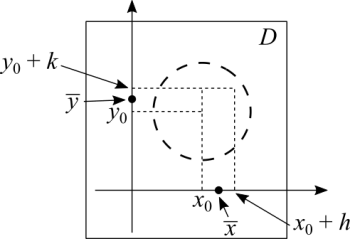
Com o domínio aberto existe uma bola aberta com centro em [math]\displaystyle{ (x_0,y_0) }[/math], em [math]\displaystyle{ D }[/math]. Sejam [math]\displaystyle{ h }[/math] e [math]\displaystyle{ k }[/math] tais que, [math]\displaystyle{ (x_0 + h,y_0 + k) }[/math] pertença à bola. Temos que:
[math]\displaystyle{ f(x_0 + h, y_0 + k) - f(x_0, y_0) = \underbrace{f(x_0 + h, y_0 + k) - f(x_0,y_0 + k)}_{\text{I}} + \underbrace{f(x_0,y_0 + k) - f(x_0,y_0)}_{\text{II}} }[/math]
Observe o gráfico acima e localize os pontos. É bastante claro a localização de cada um. Estamos assumindo que a função é diferenciável, o que implica em ser contínua. Se você seguir as coordenadas de cada ponto não encontrará "buracos" dentro do círculo. O que significa que as derivadas parciais são contínuas. Quando nos deslocamos paralelamente a um eixo estamos considerando derivadas parciais, que é o que o gráfico acima mostra com linhas tracejadas.
Com derivadas parciais uma variável é tratada como constante, portanto [math]\displaystyle{ G(x) = f(x, y_0 + k) }[/math]. (caso você esteja confuso, o [math]\displaystyle{ x }[/math] à esquerda não é mesmo da direita) Com o TVM podemos afirmar que existe um [math]\displaystyle{ \bar{x} }[/math], entre [math]\displaystyle{ x }[/math] e [math]\displaystyle{ x + h }[/math], tal que
[math]\displaystyle{ (\text{I}) = G(x_0 + h) - G(x_0) = G'(\bar{x}) h = \frac{\partial f}{\partial x}(\bar{x}, y_0 + k) h }[/math].
Agora repita para (II)
[math]\displaystyle{ (\text{II}) = \frac{\partial f}{\partial y}(x_0, \bar{y}) k }[/math].
Começamos com um ponto e um incremento para a primeira variável e outro incremento para a segunda variável. Este é o mesmo conceito de um vetor, porque na geometria analítica definimos um vetor com dois pontos. Se você olhar para trás, tínhamos uma expressão que era semelhante à derivada direcional, exceto que não nos importamos com uma direção específica agora. O que nos importa agora é a continuidade das derivadas parciais.
Conceitualmente chegamos numa equação que representa um vetor e a soma das duas componentes deste:
[math]\displaystyle{ f(x_0 + h, y_0 + k) - f(x_0, y_0) = \frac{\partial f}{\partial x}(\bar{x}, y_0 + k)h + \frac{\partial f}{\partial y}(x_0, \bar{y})k }[/math]
Subtraia [math]\displaystyle{ \frac{\partial f}{\partial x}(x_0,y_0)h + \frac{\partial f}{\partial y}(x_0,y_0)k }[/math] de ambos os lados da equação acima e realize algumas operações algébricas:
[math]\displaystyle{ f(x_0 + h, y_0 + k) - f(x_0, y_0) - \frac{\partial f}{\partial x}(x_0,y_0)h - \frac{\partial f}{\partial y}(x_0,y_0)k = }[/math]
[math]\displaystyle{ \left[\frac{\partial f}{\partial x}(\bar{x}, y_0 + k) - \frac{\partial f}{\partial x}(x_0,y_0)\right] h + \left[\frac{\partial f}{\partial y}(x_0, \bar{y}) - \frac{\partial f}{\partial y}(x_0,y_0)\right]k }[/math]
Se você se lembra da derivada direcional e olhar com atenção, o lado esquerdo da equação tem os termos [math]\displaystyle{ -Ah - Bk }[/math], onde A e B são as taxas de variação em cada direção. Agora se fizermos [math]\displaystyle{ (h,k) \to (0,0) }[/math] a equação acima se reduz a [math]\displaystyle{ f(x_0 + h,y_0 + k) - f(x_0,y_0) = 0 }[/math], que é a mesma ideia de quando queremos provar que a função é contínua num ponto. Também temos que lembrar que a derivada é um limite, então
[math]\displaystyle{ \left|\frac{f(x_0 + h, y_0 + k) - f(x_0, y_0) - \frac{\partial f}{\partial x}(x_0,y_0)h - \frac{\partial f}{\partial y}(x_0,y_0)k}{||(h,k)||}\right| \leq }[/math]
[math]\displaystyle{ \left|\frac{\partial f}{\partial y}(\bar{x},y_0 + k) - \frac{\partial f}{\partial x}(x_0,y_0)\right|\frac{|h|}{\sqrt{h^2 + k^2}} + \left|\frac{\partial f}{\partial y}(x_0,\bar{y}) - \frac{\partial f}{\partial y}(x_0,y_0)\right|\frac{|k|}{\sqrt{h^2 + k^2}} }[/math]
Funções da forma [math]\displaystyle{ \frac{x^2}{x^2 + y^2} }[/math] são limitadas, da mesma forma que o seno ou cosseno. O numerador nunca será maior do que o denominador. Caso você esteja confuso, [math]\displaystyle{ \sqrt{h^2 + k^2} }[/math] representa o raio de uma bola aberta do diagrama do início da página. As derivadas parciais são contínuas em [math]\displaystyle{ (x_0,y_0) }[/math]. Portanto, o lado direito da equação deverá ser zero quando [math]\displaystyle{ (h,k) \to (0,0) }[/math].
[math]\displaystyle{ \lim_{(h,k) \ \to \ (0,0)} \frac{f(x_0 + h, y_0 + k) - f(x_0,y_0) - \frac{\partial f}{\partial x}(x_0,y_0)h - \frac{\partial f}{\partial y}(x_0,y_0)k}{||(h,k)||} = 0 }[/math]
Com isto provamos que [math]\displaystyle{ f }[/math] é diferenciável em [math]\displaystyle{ (x_0,y_0) }[/math].
Observação: Eu segui o livro do Hamilton Guidorizzi. Outros livros como o Tom Apostol fazem a mesma demonstração mas para n variáveis.
Referência