Transforming the graph of functions

Depending on how you learned (or even worse, you didn't learn at all!) functions at school, the graphs of functions can impose a certain degree of challenge. When we are solving equations we are mostly doing calculations without thinking on the graphical representation. By combining the graphical visualization with simple arithmetic operations we can have a better understanding of the problems.

The textbooks that I know don't do much regarding translation of functions. They just throw a list of properties and their relationship with the graphs moving around, but I felt that the concept of composite function was required to avoid confusion with the minus sign and the confusion between changing the function's value (the image) and the function's argument.

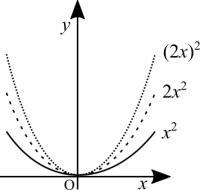
I'm mentioning linear algebra in some parts because there are some concepts from linear algebra that help to understand what is happening with functions when we transform their graphs with some operations. Often teachers of calculus mention that to multiply a function by a constant is a "linear operation or transformation" without any further explanations. Linear in here means that the deformation that you perform to a function is constant. It doesn't "destroy" the graph in the sense of bending lines or straightening curves. Non-linear means that the factor of deformation is non-constant. The function loses its original shape and proportions.

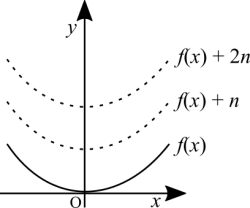
Translating the graph up / down

(Not to scale)

Take the function [math]\displaystyle{ f(x) = x^2 }[/math] for example. We want the graph to move upwards. What do we do? We add some [math]\displaystyle{ n }[/math] to the function. To add [math]\displaystyle{ n }[/math] means that, for every [math]\displaystyle{ x^2 }[/math], we want this [math]\displaystyle{ x^2 + n }[/math]. We did not change the graph's curvature nor the function's codomain. What we did was to move up all [math]\displaystyle{ y }[/math] values by some [math]\displaystyle{ n }[/math] units. In fact, it was the image that has been changed. For two variables it's the same idea. Change addition to subtraction and we move the graph down.

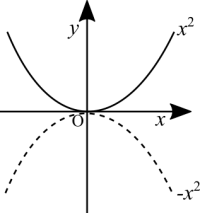
Reflecting the graph vertically

(Not to scale)

If we multiply every [math]\displaystyle{ f(x) }[/math] by -1 the function is essentially flipped upside down. Points at which [math]\displaystyle{ f }[/math] is negative are reflected to positive and vice-versa. When one function is composed (nested) in a modulus, every negative value of [math]\displaystyle{ f }[/math] is reflected to a positive one. That's why the graphs exhibits a "mirrored" behaviour. For two variables, to multiply [math]\displaystyle{ f(x,y) }[/math] by -1 has the same effect of flipping the graph upside down.

Deforming the graph

(Not to scale)

Now what about deforming the graph? We want to stretch / squeeze / shrink / enlarge it. Let's multiply the function by [math]\displaystyle{ n }[/math]. What's the difference between [math]\displaystyle{ nf(x) }[/math] and [math]\displaystyle{ f(nx) \ ? }[/math] In the first case we are making the function grow faster, [math]\displaystyle{ nf(x) \gt f(x) }[/math] for all [math]\displaystyle{ n \gt 1 }[/math] and all [math]\displaystyle{ f(x) \gt 0 }[/math] (careful with the conditions!). In the second case (careful with [math]\displaystyle{ nx^2 \neq (nx)^2 }[/math]!) we are also making the function grow faster, but at the same time we are messing with its argument as well. What happens if [math]\displaystyle{ 0 \lt n \lt 1 ? }[/math] For [math]\displaystyle{ \frac{1}{2}f(x) = \frac{1}{2}(x^2) }[/math] we are "slowing down" the speed at which the function grows. For [math]\displaystyle{ f \left(\frac{1}{2}x \right) = \left(\frac{1}{2}x \right)^2 }[/math] we are also decreasing the function's growth rate. Unfortunately I can't show an animation here, but as the constant gets closer to zero, we are "flattening" the parabola. When the sign inverts, the graph also inverts. For two variables we can deform the graph along one variable or both at the same time. However, to multiply the function by a constant is going to multiply both variables at the same time in this case. Remember, the [math]\displaystyle{ z }[/math] is dependant on each pair [math]\displaystyle{ (x,y) }[/math]. Note: in cases where [math]\displaystyle{ nf(x) = f(nx) }[/math] is true, this is one of the properties of a linear transformation in linear algebra. For two or more variables there is something called homogeneous function that I'm not going to discuss in this page.

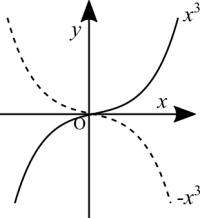
Reflecting the graph horizontally

(Not to scale)

When a function is even this operation does nothing to it. That's why for this example I'm using [math]\displaystyle{ f(x) = x^3 }[/math]. When the power is odd, parenthesis doesn't change the sign. But when the power is even, it does avoid the confusion [math]\displaystyle{ (-x)^2 \neq -x^2 }[/math]. To avoid confusion because of the minus sign I'm going to use a composite function. [math]\displaystyle{ g(x) = -x }[/math] is a function that does nothing more than to invert the sign of each number. It multiplies each number we apply to it by -1. [math]\displaystyle{ f(g(x)) = x^3 }[/math]. It's a cubic that was spin | rotated around the vertical axis. For each positive number that we input. First [math]\displaystyle{ g(x) }[/math] inverts its sign, then [math]\displaystyle{ f(x) }[/math] calculates the cube of it. In this specific case, to compose the other way around with [math]\displaystyle{ f(x) }[/math] first, yields the same result. When a function is spin | rotated around the vertical axis, there is a "hidden" composite function performing the operation that is to invert the sign of each and every argument. For two variables it's more complicated. We can invert the sign of one of the variables independently from the other or invert both at the same time. Note: you may have noticed an interesting fact. When we take an odd function and mirror it, it remains an odd function. When we take an even function and mirror it, it remains an even function. Graphically, it's all due to the fact that the functions themselves are already symmetrical in respect to one axis.

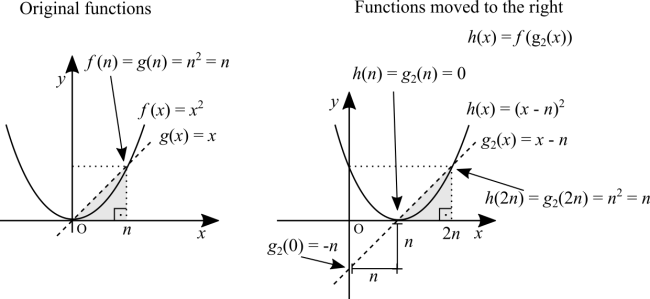
Translating the graph sideways

The first way to explain this is pretty simple. What we want to achieve is this: for each step [math]\displaystyle{ n }[/math] we take in [math]\displaystyle{ x }[/math] to the right, we want each and every point of the graph to move accordingly and not move any units up or down, nor increase or decrease the distance between them. Suppose we use [math]\displaystyle{ n = 1 }[/math]. We calculate [math]\displaystyle{ f(1), \ f(2), \ f(3), \ ... }[/math]. At the horizontal axis we are moving to the right at a constant rate of 1. At the vertical axis, however, each image is moving upwards because we are calculating [math]\displaystyle{ x^2 }[/math]. Hence, we want [math]\displaystyle{ f(1), \ f(2), \ f(3), \ ... }[/math] to not change their respective images before and after moving to the right. How do we "fix" that? We do the opposite, subtract 1 from the function's argument so that each and every image remains at their original heights. In other words [math]\displaystyle{ f(1 - 1), \ f(2 - 2), \ f(3 - 3), \ ... }[/math]. Therefore, to move the function's graph to the right by [math]\displaystyle{ n }[/math] units we change the argument to [math]\displaystyle{ (x - n) }[/math]. The same reasoning to move the function to the left, with the difference of a "+" sign.

(the graph is not to scale because it was hand draw)

[math]\displaystyle{ g_2(x) }[/math]. I used the index to differentiate the function from before and after the translation.

The second way to explain this involves rates of change and composite functions. Use the identity function, overlap it with the parabola. They intersect at the origin and at [math]\displaystyle{ n = n^2 = 1 }[/math]. See that right triangle formed with the points origin, [math]\displaystyle{ f(n) = g(n) }[/math] and [math]\displaystyle{ n \ ? }[/math] Now move the functions to the right. That triangle remains intact, which means that we didn't change the rate of change of any of the two functions. The root of both functions, however, did change from [math]\displaystyle{ f(0) = g(0) = 0 }[/math] to a new position at [math]\displaystyle{ n }[/math]. Now the rate of change of the identity function being constant means that [math]\displaystyle{ g(x \pm n) = x \pm n }[/math]. When we move it down by [math]\displaystyle{ n }[/math] units, its root also moves to the right by the same [math]\displaystyle{ n }[/math] distance. What's the function that passes through the points [math]\displaystyle{ (0, \ -n) }[/math] and [math]\displaystyle{ (0, \ n) \ ? }[/math]. It's [math]\displaystyle{ g_2(x) = x - n }[/math]. For the parabola's vertex to coincide with the root of [math]\displaystyle{ g_2 }[/math] we have that [math]\displaystyle{ f_2(g_2(x)) = (x - n)^2 }[/math]. We want both the parabola and the straight line to have a height of zero there. That's a graphical way to understand composite functions.

Moving odd or even functions around

[math]\displaystyle{ \ \ \ f(x) = f(-x) }[/math]. Even function.

[math]\displaystyle{ -f(x) = f(-x) }[/math]. Odd function.

Both odd and even functions are symmetric, but that fact alone is not what makes them odd or even!

An even function remains even if you multiply it by a constant. The same is true for odd functions. Think about it. The constant factor deforms the function, but it does preserve the symmetry in respect to the vertical and horizontal axes.

To move a function up or down may or may not preserve the fact that the function is odd or even. See how the points of the parabola behave as we move the graph up or down. It's easy to see that it remains an even function. On the other hand, the identity function loses the property of being odd if we do that.

Moving the function to the right or to the left does preserve the function's symmetry and overall shape, but the function is no longer odd nor even. Think about it. If we move a parabola sideways, we didn't change its shape. However, we messed with its argument. Take two points, [math]\displaystyle{ a \neq b }[/math], such that [math]\displaystyle{ f(a) = f(b) }[/math]. After the function is moved sideways, we no longer have [math]\displaystyle{ |a - 0| = |b - 0| }[/math]. The same happens with odd functions. That is, the distance between the two arguments is preserved when the function is moved sideways. On the other hand, the distance between one argumento and the origin and the other argument and the origin, is now different from each other.