Theorems covering limits and continuity of functions

From Applied Science

Depending on the teacher and on which type of calculus course it is being taught, those theorems may be left unproven because they require a level of abstraction that not everyone is familiar with. There is also a matter of time constrains. It's not always feasible to do the proofs.

The theorems below always assume functions to be continuous, because if they aren't continuous in some interval we are unable to state many properties. There are always two different points [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math], because if [math]\displaystyle{ a = b }[/math] we don't have an interval and cannot state anything about the function except for checking whether the function is defined there or not. The distance between the extreme points can be small or large. As long it's positive it doesn't matter. The graphs may differ from textbook to textbook and that's natural. We are taking one small part of a general idea. There is no way to plot all cases one by one, nor plot at infinity.

Before progressing to the theorems we can already make some questions: what if the function has a point in which the limit is infinity? Then the function cannot be continuous at that point. Therefore, we can't have a maximum value there because infinity is not a number. Conversely, negative infinity is not a minimum value. What if the limit doesn't exist? At best we can state that the function is bounded between two extremes, but with the limit being undefined we are unable to conclude anything from a value that we can't know for sure. Can you answer the question of which number is greater than the other if you don't know the numbers in the first place? It's impossible! By assuming the functions to be continuous in a certain interval we are ruling out some cases which would invalidate the theorems otherwise.

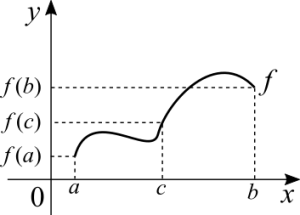
Intermediate value theorem

If [math]\displaystyle{ f }[/math] is continuous in [math]\displaystyle{ [a, \ b] }[/math] and [math]\displaystyle{ f(c) }[/math] is in between [math]\displaystyle{ f(a) }[/math] and [math]\displaystyle{ f(b) }[/math]. Then there shall exist a [math]\displaystyle{ c }[/math], in that interval, such that [math]\displaystyle{ f(c) = c }[/math].

(This is not the mean value theorem)

This theorem can be thought as an extension of the fact that in between two real numbers there is always another. In between two values of a function there is always another. Notice that this theorem only makes sense with the assumption that the function is continuous. We can't use this theorem to prove that a function is continuous! This theorem is a consequence of a function's continuity. The idea of it is similar to the mean value theorem. In between [math]\displaystyle{ f(a) }[/math] and [math]\displaystyle{ f(b) }[/math] there is going to be a value which is the average of the two. I think that this is where the confusion between the two theorems happen.

A subcase of this theorem is Bolzano's theorem. If [math]\displaystyle{ f(a)f(b) \lt 0 }[/math], then the function does have a point where [math]\displaystyle{ f(x) = 0 }[/math]. This is one of the first theorems we learn in numerical methods classes, because we need this fact to find roots of equations. One may think about higher dimensions. Bolzano's theorem only makes sense in a cartesian plane. Can we go to the other side without crossing a line? In 2D no. We need the 3D space to go to the other side without touching it. I have no idea if there is a similar theorem covering higher dimensions.

We can make a comparison here between the intermediate value theorem and the formal definition of a limit. The latter says that we begin with an epsilon given and no matter how small it is, there is a corresponding delta. The former says that if a function is continuous in between two points, then the function must also assume all values in between. In particular, one of the values is going to be the mean between the two extreme points of an interval.

Links for the proofs:

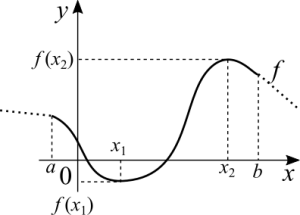
Weierstrass' extreme value theorem

If [math]\displaystyle{ f }[/math] is continuous in [math]\displaystyle{ [a, \ b] }[/math]. Then there shall exist [math]\displaystyle{ x_1 }[/math] and [math]\displaystyle{ x_2 }[/math], in that interval, such that [math]\displaystyle{ f(x_1) \leq f(x) \leq f(x_2) }[/math] for all [math]\displaystyle{ x }[/math] in [math]\displaystyle{ [a, \ b] }[/math].

(the theorem does not care about the function being constant, crescent or decrescent in between the two extremes. Don't associate the theorem to just one type of function.)

What this theorem states is that, in a closed interval, the function is going have a maximum and a minimum. The interval has to be closed because if we consider an open interval we are accepting values at which the limit may be infinity, which would invalidate the theorem. Remember that infinity is not part of the real numbers. We cannot calculate a function at infinity, but we can calculate the limit at infinity. By having the interval closed we guarantee that the function is defined and has a finite limit.

Suppose we have the function [math]\displaystyle{ f(x) = 1/x }[/math]. If the interval is open and contains the zero, we won't ever divide by zero. However, by being open we can get infinitely close to zero and this means to accept that the function is not bounded because it's going to infinity. If the interval is closed and excludes the zero, maybe it has the number 0.0001 which is finite and [math]\displaystyle{ f(0.0001) }[/math] is finite. Anything in between 0.0001 and 0 is not part of the interval.

Links for the proofs:

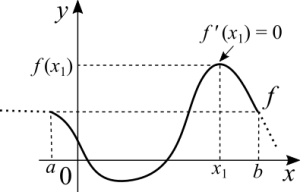
Rolle's theorem

If [math]\displaystyle{ f }[/math] is continuous in [math]\displaystyle{ [a, \ b] }[/math], differentiable in [math]\displaystyle{ ]a, \ b[ }[/math] and [math]\displaystyle{ f(a) = f(b) }[/math]. Then there shall exist a [math]\displaystyle{ x_1 }[/math], in that interval, such that [math]\displaystyle{ f'(x_1) = 0 }[/math].

(the theorem guarantees that at least one point is going to have a derivative equal to zero. There may be more than one.)

What this theorem states is that in between two points of the function, with the same height, there is going to be a point where the derivative is zero. Think about this: if the function is strictly crescent or strictly decrescent it's impossible for it to have an horizontal tangent in between two points. The theorem states that if the two extremes have the same value, either the function is constant or somewhere in between the rate of change invert its sign.

For the same reason of the extreme value theorem the interval has to be closed. Now why does it say that the function is differentiable on an open interval? Because there are functions with points where the limit exists and the function is also continuous, yet it's not differentiable. For example [math]\displaystyle{ f(x) = |x| }[/math] is differentiable everywhere, except for the origin. That's why the theorem says that the function is differentiable on an open interval. The function may be continuous at the extremes, while at the same time not differentiable there.

Links for the proofs:

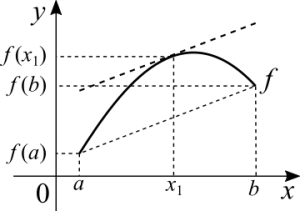
Lagrange's mean value theorem

If [math]\displaystyle{ f }[/math] is continuous in [math]\displaystyle{ [a, \ b] }[/math], differentiable in [math]\displaystyle{ ]a, \ b[ }[/math]. Then there shall exist a [math]\displaystyle{ x_1 }[/math], in that interval, such that [math]\displaystyle{ f'(x_1) = \frac{f(b) - f(a)}{b - a} }[/math] or [math]\displaystyle{ f'(x_1)(b - a) = f(b) - f(a) }[/math]

(This is not the intermediate value theorem. The name is similar but it's a different theorem. The point where the tangent is parallel to the secant does not need to be in between [math]\displaystyle{ f(a) }[/math] and [math]\displaystyle{ f(b) }[/math]. This is a confusion that can happen due to the similarity of both theorems.)

What this theorem states is that we have a secant line that passes through two points of the function. In between the two points there must be a tangent line that is parallel to the secant. The theorem doesn't state that the point is unique, there may be others. We are making the assumption that the function is differentiable, otherwise the parallel tangent line may not exist because there may be a point where the function is continuous but not differentiable. The idea is pretty similar to Rolle's theorem. In fact, Rolle is a subcase of the mean value theorem.

[math]\displaystyle{ (b - a) \neq 0 }[/math]. First [math]\displaystyle{ b \neq a }[/math], otherwise we don't have a rate of change. Second, when we calculate the limit to make the distance between the two infinitely small we never make the distance equal to zero itself.

Physical interpretation: suppose a function represents velocity in time. Suppose that during a certain interval of time the velocity goes up and down. At a certain instant it's 20 m/s and at another instant it's 10 m/s. Average velocity as we learn at school is [math]\displaystyle{ (10 + 20)/2 = 15 \ m/s }[/math]. What the theorem says about velocity is that there must be a certain instant in which the velocity is the average velocity itself. It doesn't matter how fast the velocity changes over time. What matters is that the process is continuous. In case the acceleration is zero, the average velocity should be equal to the velocity itself at all instants.

Notice that if we have a process that is discontinuous at some point we cannot use this theorem. Because the mean value could be located precisely where the function is discontinuous.

Links for the proofs:

Cauchy's mean value theorem

If [math]\displaystyle{ f }[/math] and [math]\displaystyle{ g }[/math] are continuous in [math]\displaystyle{ [a, \ b] }[/math], differentiable in [math]\displaystyle{ ]a, \ b[ }[/math]. Then there shall exist a [math]\displaystyle{ c }[/math] in [math]\displaystyle{ ]a, \ b[ }[/math] such that [math]\displaystyle{ [f(b) - f(a)]g'(c) = [g(b) - g(a)]f'(c) }[/math]

or

[math]\displaystyle{ \frac{g(b) - g(a)}{f(b) - f(a)} = \frac{g'(c)}{f'(c)} }[/math], if [math]\displaystyle{ g(a) \neq g(b) }[/math] and [math]\displaystyle{ f'(c) \neq 0 }[/math].

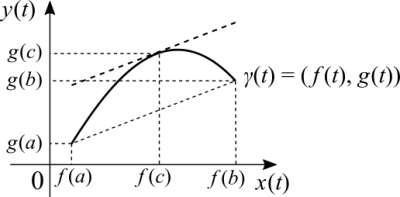
(Careful with this graph! It's [math]\displaystyle{ x(t) }[/math] x [math]\displaystyle{ y(t) }[/math], not [math]\displaystyle{ t }[/math] x [math]\displaystyle{ \gamma (t) }[/math]!)

This theorem is a generalization of the mean value theorem. Suppose we have two different functions between two points and each one obeys to the conditions of the mean value theorem. A natural question arises: if each function, own its own, is going to have a point where the rate of change is equal to the average rate of change. Is there a point in which the rate of change of each function is equal to the average rate of change of the other? Yes, there is.

Careful with the interpretation of it! Suppose that at point [math]\displaystyle{ x = c }[/math] we have that the rate of change of [math]\displaystyle{ f }[/math] is equal to the average rate of change. That doesn't imply that the same is true for [math]\displaystyle{ g }[/math]! The point where that happens for [math]\displaystyle{ g }[/math] may be somewhere else because it's a different function! What the theorem states is that both functions should have equal average rates of change. At some point in school we learn that two different sets of numbers can have the same average.

I have a textbook that presents a different interpretation. A curve can be a trajectory with each of its points given by a linear combination of more than one function, one for each coordinate. We choose two points and trace a secant line. In between the two points there must be a tangent line that is parallel to the secant. It's the same geometrical idea of the mean value theorem, except that the trajectory is a vector valued function. How do we derive a vector valued function? We derive each of its coordinates, because each one has a function of its own. At each point in the curve we have the same parameter, which is time in the case of trajectories.

Links for the proofs:

Retrieved from "https://www.0kdesign.org:443/appliedscience/index.php?title=Theorems_covering_limits_and_continuity_of_functions&oldid=2008"