Propriedades das raízes

A associação entre raiz quadrada e quadrados é natural. A raiz cúbica é associada com cubos e não há maiores complicações até aí. Com dimensões maiores perdemos a visualização geométrica e temos que nos contentar com a álgebra.

A relação entre [math]\displaystyle{ a^2 }[/math] e [math]\displaystyle{ \sqrt{a} }[/math] é a mesma que entre a exponencial e o logaritmo, um é o inverso do outro. Sempre que temos um número elevado ao quadrado, isto significa a área de um quadrado onde o lado é aquele número. A raiz quadrada calcula o lado da área daquele mesmo quadrado.

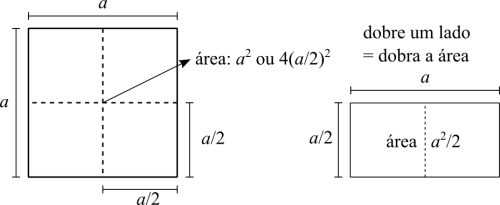
Eu acho que duas confusões acontecem aqui: uma é pensar que a raiz quadrada corta um número pela metade. A outra é pensar que a raiz quadrada acha 1/4 da área de um quadrado. Tudo envolve o número 2. Um quadrado de lado 4 tem área igual a 16. A raiz quadrada de 16 é 4. A raiz quadrada de 4 é 2. Num quadrado de área 16 cabem 4 quadrados de área 4. Agora se tentarmos o mesmo raciocínio considerando um quadrado de lado igual a 5, a raiz quadrada de 5 é irracional e não é nem metade e nem um quarto de 5. Se você observar a figura, eu usei a variável [math]\displaystyle{ a }[/math] para representar o lado. Se você substituir vários números, vai perceber que alguns são quadrados perfeitos e outros não. Em cálculo podemos estudar sequências de tais números.

A confusão mencionada anteriormente é especialmente comum na física. Porque quando temos unidades ao quadrado como [math]\displaystyle{ m^2 }[/math] e [math]\displaystyle{ m/s^2 }[/math]. Muitos erros de interpretação começam aí.

• [math]\displaystyle{ \sqrt{a} + \sqrt{b} \neq \sqrt{a \ + \ b} \iff a^2 + b^2 \neq (a + b)^2 }[/math]. Considerando [math]\displaystyle{ a,b \neq 0 }[/math]. A soma das raízes não é a raiz da soma. Reciprocamente, a soma dos quadrados não é o quadrado da soma. É fácil ver isto com os quadrados acima. Uma aplicação bem comum é na resolução das telas, monitores e fotos. Se tivermos dois monitores com a mesma resolução cada, não quadruplicamos a resolução, nós dobramos. Assim também explicamos que dobrar a largura ou altura de um terreno aumenta a área, mas menos do que se dobrarmos ambas as dimensões ao mesmo tempo. É o mesmo raciocínio informal para explicar porque aumentando o raio de um círculo, o perímetro aumenta menos do que a área. No caso de uma esfera, a área da superfície aumenta menos do que o volume.
  
  Uma outra forma de visualizar a confusão recém mencionada é fazendo isto: [math]\displaystyle{ raiz(a) + raiz(b) \neq raiz(a + b) \iff pot(a) + pot(b) \neq pot(a + b) }[/math]. Eu escrevi a mesma coisa mas usando uma notação de função não usual. Algumas funções obedecem à equação anterior, outras não. A análise funcional se ocupa de estudar quais funções obedecem à propriedade anterior.

• [math]\displaystyle{ \sqrt{a}\sqrt{b} = \sqrt{ab} }[/math]. Lembre-se que as raízes são expoentes racionais. Então [math]\displaystyle{ a^{\frac{1}{2}}b^{\frac{1}{2}} = (ab)^{\frac{1}{2}} \iff (a^{\frac{1}{2}}b^{\frac{1}{2}})^2 = ((ab)^{\frac{1}{2}})^2 \iff a^1 b^1 = (ab)^1 }[/math] prova a propriedade.
  
  
  
  
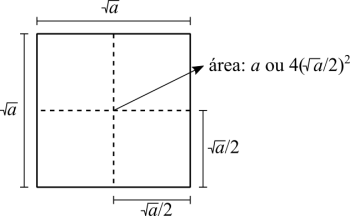
  Eu vou repetir os mesmos quadrados de antes com uma pequena alteração. Agora a raiz é o lado e a variável é a própria área. A maioria das pessoas esta familiarizada com esta propriedade [math]\displaystyle{ 2\sqrt{x} = \sqrt{2^2 x} }[/math]. Em outras palavras, colocamos um número "dentro" da raiz transformando o número numa potência enésima de acordo com o índice da raiz. Na figura anterior nos concentramos nas áreas. Vamos mudar o foco para o perímetro agora: o perímetro do quadrado grande é [math]\displaystyle{ 4\sqrt{a} }[/math]. Vamos ver o perímetro de um ladrilho agora [math]\displaystyle{ 2\sqrt{a} = \frac{\sqrt{a}}{2} + \frac{\sqrt{a}}{2} + \frac{\sqrt{a}}{2} + \frac{\sqrt{a}}{2} = \sqrt{4a} = \sqrt{4}\sqrt{a} }[/math]. Vê? A propriedade de por um número de fora da raiz para "debaixo" dela é relacionada com os perímetros, não com as áreas.
  
  Referência: Vatsal Ojha. Eu estava procurando por uma interpretação gráfica da propriedade acima e achei este nome.