Properties of the absolute value
We all learn at school that a number is either positive or negative, with positive numbers not requiring a plus sign because it's the standard everywhere in the world. We always assume a number without a sign to be positive. Now textbooks that I had at school and the teachers that I had back then would always say that modulus "erases" the sign. I always felt that operation to be meaningless because if a number has no sign, does it mean that the number is neither positive nor negative? What is it?
I remember that I struggled a lot with signs and rules. There are many youtube videos with teachers discussing precisely the signs and rules with signs. Now I can't speak for others, but maybe many people out there make this mistake [math]\displaystyle{ |a - b| = a + b }[/math]. That is, if we are told that the modulus erases the sign, then does it mean that we erase the minus sign of every operation in between the two bars? I pretty sure that the way we are told to "erase" the minus sign from numbers can very well lead to that erroneous conclusion. I have no idea and have never witnessed it to be honest, but maybe some teacher out there in the world has witnessed this [math]\displaystyle{ |2 \pm 2| = 22 }[/math]. I know it's absurd, but what if someone understood the absolute value as literally removing the sign from existence?
The way I was told what the absolute value of a number is causes more harm than any good because sometimes I wondered if there was an operation that is beyond the four basic arithmetic operations that we all know. The definition of the absolute value is a function, but we don't know that because we learn it before learning about functions.
[math]\displaystyle{ |x| = \begin{cases} x,& \ \text{if} \ x \gt 0 \\ 0,& \ \text{if} \ x = 0 \\ -x,& \ \text{if} \ x \lt 0 \end{cases} }[/math]
You may have asked about the middle case. Zero can be placed in the first or the second case, it's a matter of preference. Or we can use a third case. It doesn't change the definition in any way. A number can never be greater than or less than itself, it can only be equal to itself.
The properties
- [math]\displaystyle{ |x| \geq 0 }[/math]. A negative distance doesn't exist. It's always positive or null.
- [math]\displaystyle{ |a - b| = |b - a| }[/math]. The distance between two points does not depend on the order of the points. We have to consider three cases: both numbers are positive, both are negative or one is negative and the other is positive. Or, more generally, the difference between the two numbers can be positive, negative or null.
1st case: [math]\displaystyle{ a - b \gt 0 \implies b - a \lt 0 }[/math]. Then, [math]\displaystyle{ |a - b| = a - b }[/math] and [math]\displaystyle{ |b - a| = -(b - a) = -b + a = a - b }[/math]. (if you didn't follow, it's the definition of the absolute value itself).
2nd case:[math]\displaystyle{ a - b \lt 0 \implies a - b \gt 0 }[/math]. Then, [math]\displaystyle{ |a - b| = a - b }[/math] and [math]\displaystyle{ |a - b| = -(a - b) = -a + b = b - a }[/math].
3rd case: [math]\displaystyle{ a - b = 0 \implies a = -b \ \text{or} \ -a = b }[/math]. Then, [math]\displaystyle{ |a - b| = |b - a| = 0 }[/math].
- [math]\displaystyle{ |x| = 0 \iff x = 0 }[/math]. +0 or -0 is meaningless, zero doesn't have a sign. It doesn't make sense to think about zero as either positive or negative.
- [math]\displaystyle{ |x| = |-x| }[/math]. Reflection symmetry. It can be rewritten as [math]\displaystyle{ x = -(-x) = (-1)(-x) }[/math]. I remember making this mistake numerous times and it's to think that the property is the same as [math]\displaystyle{ -1 = 1 }[/math]. It's obviously wrong, but for the purposes of plotting graphs of functions this is exactly where a lot of people go wrong. Not because they think that a number is equal to its negative counterpart, but because they think that the two numbers yield the same position in the Cartesian plane.
- [math]\displaystyle{ |ab| = |a||b| }[/math]. Intuitively it's easy to grasp that both are equal because we aren't going to see negative numbers coming from it. Formal proof:
Let's begin stating that [math]\displaystyle{ |x|^2 = |x^2| = x^2,\ \forall x \in \mathbb{R}. }[/math] Try two numbers, one positive and one negative to check it. Or use [math]\displaystyle{ x^2 = a }[/math] to get a different view on it.
[math]\displaystyle{ x^2 \geq 0, \ \forall x \in \mathbb{R} \implies |x^2| = x^2 }[/math]. If you didn't follow this, try the substitution I mentioned above.
If [math]\displaystyle{ x \gt 0 }[/math], then [math]\displaystyle{ |x| = x }[/math]. [math]\displaystyle{ \therefore |x|^2 = x^2 }[/math].
If [math]\displaystyle{ x \lt 0 }[/math], then [math]\displaystyle{ |x| = -x }[/math]. [math]\displaystyle{ \therefore |x|^2 = (-x)^2 = x^2 }[/math]. If you didn't follow, remember that what the absolute value does to a negative number is to invert its sign. Some people may think that this step is the same as swapping out | | for ( ).
If [math]\displaystyle{ x = 0 }[/math], then [math]\displaystyle{ |0| = 0 }[/math]. [math]\displaystyle{ \therefore |0|^2 = 0^2 = 0 }[/math].
[math]\displaystyle{ |ab|^2 = (ab)^2 = a^2b^2 = |a|^2|b|^2 \Rightarrow |ab| = |a||b| }[/math]. This proves the property.
- [math]\displaystyle{ \left|\frac{a}{b}\right| = \frac{|a|}{|b|} }[/math]. We assume [math]\displaystyle{ b \neq 0 }[/math]. With a negative exponent this is the same as the property above. Let's do it:
[math]\displaystyle{ \left|\frac{a}{b}\right| = |ab^{-1}| = |a||b^{-1}| }[/math]
From the previous proof: [math]\displaystyle{ |b||b^{-1}| = |bb^{-1}| = |1| = 1 }[/math], we have [math]\displaystyle{ |b^{-1}| = |b|^{-1} }[/math]
Conclusion: [math]\displaystyle{ |a||b^{-1}| = |a|(|b|^{-1}) = \frac{|a|}{|b|} }[/math].
- [math]\displaystyle{ |a - b|^2 = (a - b)^2 }[/math]. This property says that the area of a square can never be negative. Because the distance between two points cannot be negative. If we calculate the difference between two numbers, it can be either positive or negative, assuming they are different numbers. But since we are calculating the area of a square, it won't be negative.
[math]\displaystyle{ |a - b|^2 = |a - b||a -b| = |(a - b)^2| = (a - b)^2 }[/math].
- [math]\displaystyle{ \sqrt{x^2} = |x| }[/math]. Any (real) number, negative or not, squared, is positive because it means the area of a square. This happens to coincide with the definition of the absolute value. Both areas and lengths are always positive.
We know that [math]\displaystyle{ x^2 \geq 0, \ \forall x \in \mathbb{R} }[/math] and from the previous properties [math]\displaystyle{ |x|^2 = x^2 }[/math] it follows that [math]\displaystyle{ \sqrt{x^2} = |x| }[/math]. (to take the square root on both sides is the same as to calculate the 1/2 power on both sides).
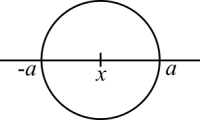
- [math]\displaystyle{ \text{If} \ a \gt 0, |x| \lt a \iff -a \lt x \lt a }[/math]. There are two graphical ways to visualise this. One is a number line. Suppose [math]\displaystyle{ a = 10 }[/math]. Then [math]\displaystyle{ x }[/math] is bounded between two extremes, 10 and -10. For example, we can think on 9.999 (don't write .999...!!). Any number in between the two extremes satisfy that property.
The other way is to view a circle with the center at [math]\displaystyle{ x }[/math] and radius equal to [math]\displaystyle{ |a - x| }[/math]. The property states that [math]\displaystyle{ x }[/math] is located anywhere along the circle's diameter, except for the two extremes, [math]\displaystyle{ -a }[/math] and [math]\displaystyle{ a }[/math]. How to prove that that property is true? We use the definition of the absolute value:
If [math]\displaystyle{ x = 0 \implies |a| \gt 0 }[/math]. Else [math]\displaystyle{ x = a = 0 }[/math], but we began assuming that [math]\displaystyle{ a \gt 0 }[/math].
If [math]\displaystyle{ x \gt 0 }[/math] there comes the question [math]\displaystyle{ x \gt a }[/math] or [math]\displaystyle{ x \lt a }[/math]? Let's ignore the first case because we want to prove that the [math]\displaystyle{ x }[/math] is somewhere along the circle's diameter, not outside the circle:
[math]\displaystyle{ 0 \lt x \lt a \implies 0 \lt |x| \lt a \iff -a \lt x \lt a }[/math]. Then we can conclude that [math]\displaystyle{ -a \lt 0 \lt x \iff |x| \lt a }[/math]. (if you didn't follow, remember that [math]\displaystyle{ a }[/math] is positive and therefore, [math]\displaystyle{ x }[/math] is also positive. Choose two positive numbers and see for yourself on the figure above)
Now there is the unsolved [math]\displaystyle{ x \lt 0 }[/math] case (we first considered the positive, now comes the negative):
[math]\displaystyle{ |x| \lt a \implies -x \lt a }[/math] and [math]\displaystyle{ x \lt a }[/math]. But we can invert the sign as such [math]\displaystyle{ x \gt -a }[/math]. Both the previous cases are one [math]\displaystyle{ -a \lt x \lt a }[/math]. We proved that [math]\displaystyle{ |x| \lt a \implies -a \lt x \lt a }[/math].
Now the reversed implication:
If [math]\displaystyle{ x \gt 0, \ |x| = x }[/math]. Then [math]\displaystyle{ x \lt a }[/math].
If [math]\displaystyle{ x \lt 0, \ |x| = -x }[/math]. Then [math]\displaystyle{ -x \lt a }[/math] is equal to [math]\displaystyle{ x \gt -a }[/math] and [math]\displaystyle{ |x| \lt a }[/math].
Conclusion: [math]\displaystyle{ -a \lt x \lt a \implies |x| \lt a }[/math].
- [math]\displaystyle{ |a + b| \le |a| + |b| }[/math]. Triangle inequality. In Euclidean geometry, the sum of the lengths of two sides of a triangle can never be less than the length of the third side. Or, from another point of view, if we divide a line in two parts, the sum of the parts cannot be greater than the original line. There is more than one way to prove it, I'll show one:
[math]\displaystyle{ -|a| \le a \le |a| }[/math]
[math]\displaystyle{ -|b| \le b \le |b| }[/math] (a number is bounded between itself and its opposite)
Add up both: [math]\displaystyle{ -|a| - |b| \le a + b \le |a| + |b| }[/math]
The previous property states that [math]\displaystyle{ |a| \le b \iff -b \le a \le b }[/math]
Conclusion: [math]\displaystyle{ |a + b| \le |a| + |b| }[/math]