Polar coordinates

The Cartesian system of coordinates, or rectangular coordinates, is the most widely known because it's the most common. We subdivide the plane with columns and rows and each position is located by knowing the column and row. At school most people should have had a teacher who compared the Cartesian system with the game Battleship or a chessboard.

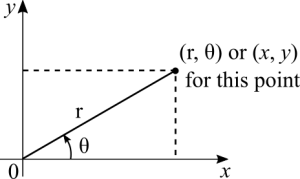
The Cartesian system is easier to understand because in it we have left and right, up and down, exactly as in daily life. It's natural to think in terms of North - South, West - East directions. There is another system of coordinates called Polar Coordinates that locates points with two coordinates: distance and angle. If we add a second angle to the Polar system we get the spherical system for 3D. If we take the polar system and add depth, a z axis, we have the cylindrical coordinate system.

Going beyond and we can naturally extend the Cartesian and Spherical coordinate systems to even higher dimensions. A 4D space has four linearly independent axis, but we cannot draw or see it.

There is one important fact that relates both coordinate systems, Polar and Cartesian. Each point has a unique location in the space and this fact is what makes it possible to overlap both systems. Each point can have its position described by both systems at the same time.

In linear algebra we learn the concept of linear dependency and with it we learn that as long as we have two linearly independent vectors, the coordinate system of a plane or space if we have a third vector, doesn't have to be rectangular. One axis can very well be angled. We just don't see such coordinate system very often because the fact that the axes are perpendicular to each other makes our lives easier. The unit circle and the dot product really depend on the fact that the axis are perpendicular to each other.

Conversion between Polar and Cartesian systems

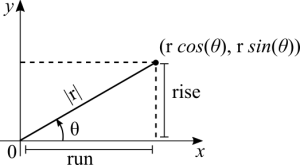
Let's take a look at the same figure, but now with attention to sine and cosine (I'm assuming that you know how to read the unit circle):

Conversion from Polar to Cartesian:

[math]\displaystyle{ \sin(\theta) = \frac{\text{rise}}{r} \iff r \sin(\theta) = \text{rise} }[/math]

[math]\displaystyle{ \cos(\theta) = \frac{\text{run}}{r} \iff r \cos(\theta) = \text{run} }[/math]

(Careful! The division by the radius is allowed because we are considering that the distance is never negative nor null. The Cartesian coordinates themselves can be negative numbers, but a distance is never negative.)

Conversion from Cartesian to Polar:

The reverse process, from Cartesian to Polar, has an added complexity caused by some issues related to angles.

[math]\displaystyle{ |r| = \sqrt{x^2 + y^2} }[/math]. This pretty natural as the length of the radius is a distance and that distance is also the hypotenuse of the right triangle shown in the figure above. More than that, it's also the norm of a vector. What vector? The displacement vector, or position vector. Remember that vector + point = point.

[math]\displaystyle{ \theta = \arctan \left(\frac{y}{x} \right) }[/math]. Now this is the issue with converting from polar to Cartesian. An angle is a ratio, the rise / run ratio on a right triangle. [math]\displaystyle{ \tan(\theta) }[/math] is the function that relates the angle with the ratio. The inverse of that, the inverse function that relates the ratio with the angle, is the arctangent function. Notice how [math]\displaystyle{ x }[/math] cannot be zero, else we have a division by zero. There is the problem, [math]\displaystyle{ y }[/math] can be zero, which means that are infinite pairs [math]\displaystyle{ (0,y) }[/math] for which the formula won't work.

Another point to make is that [math]\displaystyle{ \arctan(y/x) }[/math] is really a composite function and with two variables. Some textbooks leave the formula as [math]\displaystyle{ \tan(\theta) = y/x }[/math] to avoid having to use the inverse trigonometric function and because its easier to remember the right triangle and make the association.

At (0,0), zero distance and zero angle, we are at the origin and x = 0 and y = 0. The indeterminate 0/0 form in here means that we cannot know which direction a point is facing if we have a point at the origin. Unless the point travels one step in any direction we can't know which direction it is facing.

Polar graphs

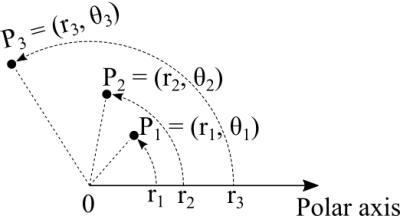
With the Cartesian system we need two axis, X and Y, horizontal and vertical. With the polar system we need just one axis, the polar axis. It's not wrong to have two axis, it's just that by having two perpendicular axis it's easier to find the right angle and its multiples. The standard adopted in mathematics is to measure angles anti-clockwise (I have no idea if there is a country in which they do it clockwise). As such we trace a lonely axis to the right, following the same direction of the number line. From zero to infinity we have positive distances. That's the radius or the distance from the origin to a point. Then, as we rotate anti-clockwise, we describe a circle with that radius.

The most common confusion here is to think that we walk to the right, to the left, up and down with polar coordinates. That's not how it works! Every point is given by some distance over the polar axis and then rotated anti-clockwise following some angle. The best tool to understand this is to know how to use a compass to trace circles. To avoid confusing the order of the coordinates think about the compass. First you "open" it, define the circle's radius, then you rotate it. If you try to trace a circle without defining the radius first, it's going to be a dot.

Sometimes we have such a strong belief that a function's image can never be a circle that it takes some time to look at a graph in polar coordinates and understand that, in polar coordinates, a function's image can be a circle.