Partial derivatives and direction

The idea of partial derivatives is pretty similar to the regular derivative. The concept of a derivative is that of a rate of change. For multivariable functions we have to look for rates of change on a per variable basis. That's the meaning of "partial". A multivariable function can increase in one direction and decrease in another. We have to study how the function behaves for each direction separately from the others. With the axes being linearly independent we can differentiate in respect to one variable, while the others are treated as constants. The same discussion that we make about conditions for differentiability for a single variable can be made for many variables, albeit we are required to rely on linear algebra to do it properly.

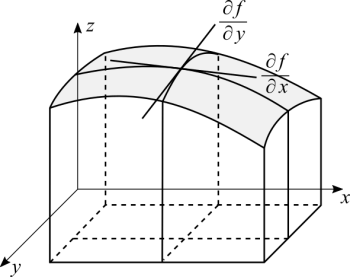
Graphically we have this:

See that partial derivatives, graphically, mean that we are considering derivatives parallel to each axis. While we "walk" parallel to an axis we have variations in one direction but not in the others. That's why multivariable calculus requires vectors, because we have multiple variables and multiple directions. Notice that to differentiate in respect to one variable we keep a constant distance from the axis we are parallel to. The distance itself doesn't matter as long as it is a constant. That's the graphical meaning of treating a variable as a constant.

We can easily extend the same limit that we have to define the derivative for a single variable to many variables:

[math]\displaystyle{ \frac{\partial f}{\partial x} (x, y) = \lim_{x \ \to \ p} \frac{f(x, \ y) - f(p, \ y)}{x - p} }[/math] or [math]\displaystyle{ \lim_{h \ \to \ 0} \frac{f(x + h, \ y) - f(x, \ y)}{h} }[/math]

Notice that one variable is kept fixed. We don't have any increments for it. We are already using the notion of direction by having derivatives parallel to an axis. With a slightly modification to the definition of a partial derivative we define directional derivatives, which allow us to calculate the rate of change for directions that aren't parallel to an axis.

Notation: assuming [math]\displaystyle{ z = f(x,y) }[/math]

[math]\displaystyle{ f_x(x,y) = f_x = \frac{\partial f}{\partial x} = \frac{\partial}{\partial x} f(x,y) = \frac{\partial z}{\partial x} = f_1 = D_1 f = D_x f }[/math]

Repeat for the other variables. The index number 1 means 1st variable. Then there are the 2nd, 3rd, and so on.

Directional derivative

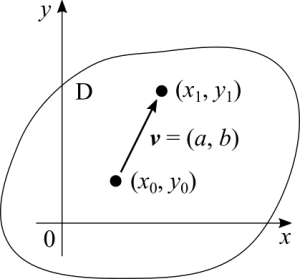
With one variable we choose a point, take a step forwards to the next point and then calculate a limit as the distance between the two points go to zero. That's the derivative for one variable. We don't use vectors because we don't need to. For two and more variables we choose a point and then the next point can be in any direction, as long as both points are part of the function's domain. Which direction? We need a vector to know it (one is required to know the operation point + vector to understand the directional derivative):

We have:

[math]\displaystyle{ \overrightarrow{v} }[/math] is some unit vector in any direction. It's important to note that the magnitude or modulus of it is 1 because we need the direction, not the intensity. If you don't know or don't remember, an unit vector has each of its coordinates divided by the vector's magnitude or norm. If we forget to normalize the vector the resulting rate of change is going to be wrong.

[math]\displaystyle{ (x_0 + a, \ y_0 + b) = (x_1, \ y_1) }[/math]

Calculating the function at those points:

[math]\displaystyle{ f(x_0 + a, \ y_0 + b) }[/math]
[math]\displaystyle{ f(x_0, \ y_0) }[/math]

Now we have the two points required to calculate the same limit of a derivative (for more than two variables it's the same thing, except that are more coordinates per point):

[math]\displaystyle{ \frac{\partial f}{\partial \overrightarrow{v}} (a, b) = \lim_{h \ \to \ 0} \frac{f(x_0 + ha, \ y_0 + hb) - f(x_0, \ y_0)}{h} }[/math]

From the derivative's definition, remember that [math]\displaystyle{ h }[/math] is some (positive) increment. We are taking the same increment in both axis at the same time.

The other way to write a derivative for a single variable involves a division by [math]\displaystyle{ x - p }[/math]. For two variables we can't divide by [math]\displaystyle{ (x,y) - (p_x, p_y) }[/math] because the operation of difference between points doesn't exist. To divide by a vector is also an operation that doesn't exist. Moreover, that's not the correct way to calculate a distance between two points. Notice that [math]\displaystyle{ h }[/math] in the limit above represents the distance between the points of the function, irregardless of the derivative's direction. By looking at the rate of change from one point towards another we are already considering two dimensions only, a rise and a run.

Using limits to calculate derivatives for one or many variables takes time. For two and more variables we can skip computing the limit too. I'm going to resort to vectors to explain, conceptually and omitting the formalism, that we can compute directional derivatives faster by doing a sum of partial derivatives, one for each coordinate. In physics and in mathematics we learn that any vector in an euclidian space can be decomposed as a sum of one component per dimension. For example: [math]\displaystyle{ \overrightarrow{v} = \overrightarrow{v}_x + \overrightarrow{v}_y + \overrightarrow{v}_z }[/math]. Each coordinate can have its own rate of change and a particular function to describe the motion in that direction. We can easily interpret directional derivatives as a sum of partial derivatives, one for each variable or coordinate in the same way we visualize vectors as a sum of its components.

[math]\displaystyle{ \frac{\partial f}{\partial \overrightarrow{v}}(a,b) = \frac{\partial f}{\partial x}a + \frac{\partial f}{\partial y}b }[/math]

Note: the computation's result is a scalar, because a rate of change is a scalar quantity, not a vector.