Linear vs. Non-linear relationships

I think that a lot of mistakes that happen are related to relationships that are linear, whereas others are non-linear. Linear is easy to understand because the increments follow intuition. To think that a relationship is linear when it's not is the source of one of the most common mistakes.

One bottle of water weights x units. Therefore 10 bottles of water weight 10x units. A factory with 100 employees manufactures 1000 products per day. Therefore two factories with 200 employees manufacture 2000 products per day. If turning on the air-conditioner for 10 hours a day adds up to a cost of x $ by the end of the month, then running it for 5 hours a day should cut the costs in half.

10 people - 30 units of something
42 people - x units of something

Do the cross product and solve for x. We learn that before leaning about functions and that leads to a misconception that is to think that whenever some quantity relates to another, with one being proportional to the other, then we can (we can't!!) assume that the same proportion can be extrapolated for other quantities. The only case in which we can do it is when the rate of change is constant. Else, we can't solve it like that because we can't assume that there is a linear function underneath.

The linear function that we have in this problem is: ten people are the independent variable, 30 units of something the dependent variable. Because the quantity of something clearly depends on the number of people. The ratio people / people should be equal to the ratio of units / units. In other words, we incremented the number of people by some percentage, which should be the same percentage for the increment in units of something. Geometrically we have the same concept of the tangent line when we talk about derivatives.

Ten people working for 8 hours a day, during 27 days, produce something. Now reduce the number of people from ten to eight and increase the number of hours from 8 to 9. The question is: how many days does 8 people, working for 9 hours per day, are going to take to produce the same result or quantity of something as 10 people, working for 8 hours for 27 days?

10 people - 8 hours per day - 27 days
8 people - 9 hours per day - x days

This problem is still a linear relationship, except that there are two variables now. The first reasoning that we can correctly have is that the workload per person has increased, by how much we don't know yet. What we have now is a ratio of another ratio. Let's think that people x time = workforce. The exercise tells that less people working for more hours are going to have the same production output, which could be thought as some index number.

[math]\displaystyle{ 10 \cdot 8 \cdot 27 = 8 \cdot 9 \cdot x }[/math] (notice that both sides of the equation have the same units, whichever they are)

[math]\displaystyle{ x = 30 }[/math] days.

It's better to solve such problems by using a reasoning that relates to statistics or economics than to rely on rules.

Before jumping into the conclusion "multiply everything on both sides". Let's take a second to read. In physics we have that average speed is "meters per second". Therefore, people per hours per days is: [math]\displaystyle{ \frac{\text{people}}{\text{hours} \cdot \text{days}} }[/math]. Sometimes we try to memorize what is directly proportional and what is inversely proportional that we forget the words themselves.

Note: this type of problem is a bit misleading because it's doing an oversimplification about life. When we have people as variables it's not always true that more people produce more and fewer produce less. There are tons of examples from real life where relationships aren't, can't and shouldn't be treated as linear relationships. Think about ecology. The relationships between the environment and life are extremely nonlinear.

A question that may arise here: is a ratio the same as a function? No. If we do a simple division A / B that's a quotient of some quantity by another quantity. It's a synonym for a proportion. To have a function we'd have to have a relationship between variables, not two fixed numbers. However, in higher level mathematics an operation such as addition can be associated to a function. So can the operation of dividing a number by another.

Non-linear relationships

Suppose you are presented a table that depicts the number of car accidents in a city in regards to the number of cars in the same city. Suppose that the table shows a positive association between numbers of cars and accidents, meaning that they both go up or down over time. At the origin we would obviously see zero accidents for zero cars. Now the question: can we extrapolate that as the number of cars increase over the years, the number of accidents should also increase? The answer would naturally be yes and we'd naturally expect even more accidents for each increment in the number of cars. However, there is bias involved here! What if the cars have technological advances that prevents accidents? What if the drivers are better trained? That is the whole problem of biased reasoning. Sometimes what we expect is not what we see. There is one such example that people commonly learn at school: the Malthus growth model that expects population growth to be exponential without taking into account many factors that would prevent it from happening.

Suppose a virus infects one person. That person can infect at least one more person. This is usually a case of exponential growth. That is, one person infects multiple others and we have a chain reaction that quickly explodes in quantity. Even though the model is exponential, there are some variables that are very hard to put in the equation. A person may infect zero others because that person lives alone and far away from others for example. The body of each person reacts differently to the same virus. The virus outbreak may coincide with summer or winter and the season has an impact on how fast the virus spreads. Sometimes we disregard some variable because we think it has little importance and we err because of that. It's very common to overestimate or underestimate the variables in play.

Suppose we have a relationship that is how much water evaporates per day in regards to the volume of a lake. This is probably not a linear relationship and we are also oversimplifying the problem. Volume by itself is not a good variable to predict how much water evaporates. Surface area is better for that. And the equation is more complicated than we would otherwise have thought because we have to consider moisture, wind speed, temperature, solar radiation and other factors. The model for that is really not that simple. The mathematical models behind climate prediction are complicated because they include many variables and their relationships are often non-linear.

I think the easiest equation of all non-linear relationships is [math]\displaystyle{ f(x) = x^2 }[/math]. For each unit we increment to the side of a square, the area increases by the square of it. Think about cubes and the volume grows even faster than that.

There is a very simple demonstration of a non-linear relationship using the unit circle. You can do it with a calculator too.

	sin(x)	cos(x)
10°	0.174	0.985
20°	0.342	0.94
30°	0.5	0.866

Notice that we took steps at a constant rate for the angle, but the value's of sine and cosine didn't increase with the same ratio.

Linear graph

To say that we have a constant rate of change can mean two things: the rate of change is positive or negative; or the rate of change is zero. That's a very common source of mistakes! Without more information we don't know whether the function is increasing, decreasing or neither.

Let's say we have a free fall problem. Gravity for most daily life purposes is a constant force. It doesn't matter if we are at ground level or flying at 10 km of altitude. For distances between planets or stars we can't treat gravity as a constant force because with large distances the force decreases. Suppose a person jumps from a plane flying at 2 Km of altitude, parallel to the ground. The initial vertical velocity is zero. Over time the person accelerates. Without numbers, what we can already assume is that the acceleration is positive because the person is falling and gaining velocity.

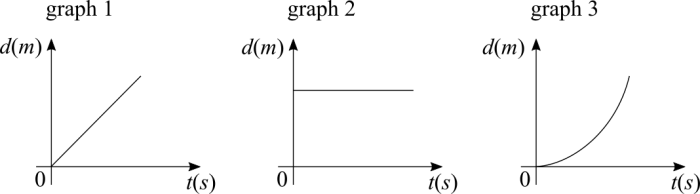
Which graph better represents acceleration x time during a free fall?

The first one could be the result of reversing the orientation of the vertical axis, but it's also a misconception. With the person falling down, one could naturally think that the graph that best describes such motion is a straight line going down. The question is about acceleration, not a trajectory!

The third one is a confusion between velocity and acceleration. We often use both interchangeably in daily life without much trouble. But we often also forget that acceleration due to gravity is a constant. Velocity is increasing during the free fall, but the acceleration is not.

The correct graph for acceleration x time for free fall is graph 2.

Non-linear graph

Now which graph better represents distance x time during a free fall?

A common mistake is to make the association between a trajectory that is a straight line and the graph. The parabola means that the rate of change of the distance from the starting position is not linear. For each instant of time, the distance increases with the square of it. I think that this is where some confusion happens. Distance is measured in meters or any multiple of it. The fact that the variation of distance over time is non-linear is not related to the unit having or not having a square in it. Over time the velocity increases during the free fall. As such, for each second that passes, the distance travelled keeps increasing faster and faster.