Linear algebra and deforming graphs of functions

In calculus we don't study linear transformations, but to deform a graph while keeping the roots of the equation, that's a concept that linear algebra studies more thoroughly. If you ever wondered at school why [math]\displaystyle{ x^2 - 6x + 5 = 0 }[/math] and [math]\displaystyle{ 3x^2 - 18x + 15 = 0 }[/math] are two different equations and yet have the same roots. The reason for that lies in linear algebra. I don't remember the teachers that I had at high school ever mentioning this.

Note: before progressing further, one may have asked "What if the graph of a function is moved around without distorting it?". What we are going to see and discuss below are cases of transformations that are not moving the graph around and keeping its shape. We are distorting it along one or both axis in two fashions: constant and non-constant.

It's a pretty abstract concept that is behind the above question. When we plot graphs that aren't functions, such as circles, the XY Cartesian plane has two independent variables. To plot functions on the other hand, has this [math]\displaystyle{ y = f(x) }[/math] relationship. What we have is not two independent axis, but one axis that depends on the other. Without discussing the definition of vector spaces, we can think on the plane on which the function's graph is plotted as a space. When we deform the axes we are deforming the whole space. The idea is more or less similar to those illustrations that depict the shape of the universe or attempt to explain how gravity deforms the space.

When we move a circle around on the Cartesian plane, one variable is not dependant on the other. With graph of functions this operation is way more complex. With one variable being dependant on the other, to move the graph around the space without deforming the graph is the same as changing the underlying equation that ties the argument to the function's value. By changing the equation we are changing the description of whatever process it's representing. It's a completely different function which may very well have lost its original interpretation after transforming the graph like that.

Constant deformation in one dimension

Notice how the line below is the same as the one above, except that the distance between each point has increased (at a constant rate!!). Imagine that line represents a ruler. As long as the whole world is using rulers with the same proportion, it doesn't matter if we are using the one above or the one below. What matters is the standard. Having standard measures for everything is a problem that physics has to solve.

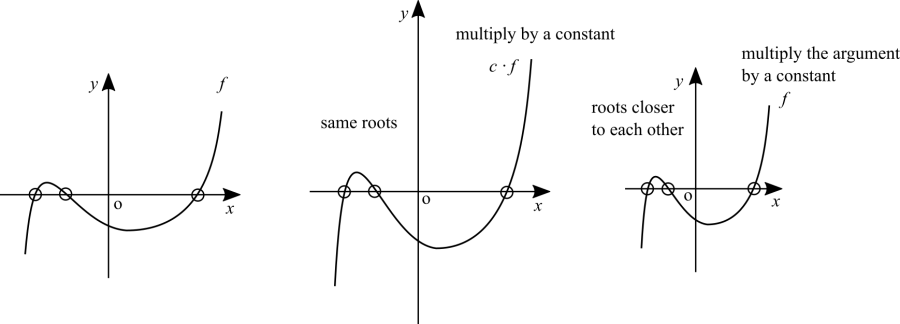
Constant deformation in two dimensions

Now in 2D. When we multiply a function by a constant, we are essentially elongating | contracting the vertical axis. That's why the roots remain the same. If we use a linear function as an argument for another, we are essentially elongating | contracting the horizontal axis. This transformation, however, does change the distance between the roots.

Can a straight line be deformed into a parabola with just the operation of elongating | contracting the axes? That's not possible. The reason for that is that we need to really distort the axes in a non-linear fashion. That is, in a non-constant rate. The reverse process, to straighten a parabola into a straight line, is also impossible without deforming the axes with a non-constant rate.

Take the number line and square the natural numbers: 1, 4, 9, 16, ... How do we bring the distance between each number back to a constant rate? We take the square root of each number. We've just discussed the concept that is: when we have a function and use its inverse as the argument, the resulting graph couldn't be anything other than a straight line! To put it into a different perspective: the rate of change of a function can be interpreted as being analogous to what acceleration is to velocity in physics. If we have a function that increases with a certain rate, to make it a straight line we have to use a function which happens to decrease at that exact same rate. If it decreases at a different rate, the graph won't be a straight line.

Non-constant deformation in one dimension

(I used letters to avoid confusion with numbers as the distance between each point is now no longer constant)

Notice how the points are no longer kept at a constant distance from each other. This is no longer a linear transformation. This is what happens if we use a non-linear function as an argument for another. The horizontal axis is deformed with a non-constant rate. For example [math]\displaystyle{ f(x) = \sin(x^2) }[/math].

If you ever had experimental physics classes or just saw a graph with a non-constant scale, that's because it's not a linear scale. One example is having the vertical axis to be in powers of ten. If you take a ruler and measure the graph you won't be able to draw conclusions from your measures because you are using a ruler that has a linear scale. Powers of ten are commonly used to make the graph easier to plot and read with things that involve large quantities or the rate of change increases | decreases a lot over time. Example: distance between stars, world's population or the number of trees.

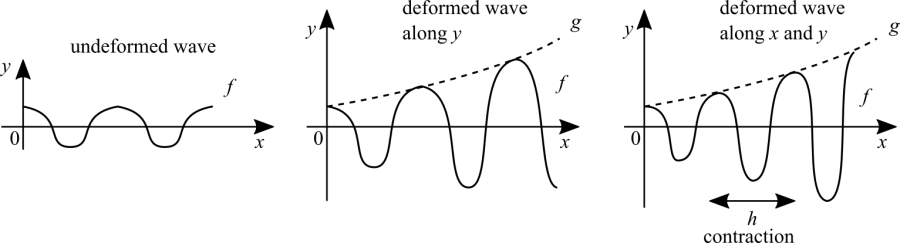
Non-constant deformation in two dimensions

Now the same non-linear transformation in 2D. That's why multiplying a function by some other function such as [math]\displaystyle{ x^2 }[/math] or [math]\displaystyle{ \sin(x) }[/math] is not a linear transformation. We are deforming the function in a way that the roots are displaced from their original points. Functions by themselves can be interpreted, graphically, as patterns. When we take some picture and rotate, stretch, blur, etc it. The software that does that is applying calculations to achieve the desired effect that are really concepts from linear algebra. To study those patterns is not something that we learn in calculus.

Search for some Op Art depicting checkerboard patterns. They are a practical example of a non-linear transformation. Another example is swimming pools. Due to the light's refraction the image that you see through the clear water is distorted. That's also another non-linear phenomena.