Limites no ou com infinito
Em cálculo não estamos preocupados com a contagem de elementos de um conjunto. O que fazemos é calcular limites que não tem extremidades, limites que divergem para o próprio infinito. Ou então calcular limites que convergem para um número, qualquer quantidade finita.
Algumas pessoas podem achar os limites um pouco contraditórios no sentido de que temos um número de um lado e algo que não é um número do outro. Eu acho que é aqui que algumas pessoas dão um salto de fé. Se a pessoa é incapaz de compreender um limite, pode ser que ela aceite os resultados ou negue-os na fé.
Assíntotas
Para os propósitos do cálculo e da geometria analítica as assíntotas são linhas tracejadas que representam uma borda. A curva esta convergindo em direção aquela borda no infinito. Não há muito que se faz com as assíntotas em cálculo, exceto traçar gráficos. A diferença entre [math]\displaystyle{ f(x) = x^2 }[/math] e [math]\displaystyle{ f(x) = 1/x^2 }[/math] é que no primeiro não temos um assíntota, enquanto no segundo temos. A assíntota sempre representa um limite, a função não vai ultrapassar aquele limite. Para funções de duas variáveis a ideia é a mesma, exceto que teríamos um plano no lugar de uma reta.
Limites que vão para infinito
[math]\displaystyle{ \lim_{x \ \to \ \infty} x^2 = \infty }[/math] porque a função pode crescer indefinidamente. [math]\displaystyle{ \lim_{x \ \to \ \infty} \frac{1}{x} = 0 }[/math] porque estamos dividindo um número por outro muito grande, ou em partes cada vez menores sem fim. Há uma forma rigorosa de provar que a nossa intuição esta correta em ambos os casos? Sim, há. A ideia é bastante abstrata porque todo o conceito é "há um número bem grande, então podemos adicionar um e fazê-lo ainda maior e continuar no processo indefinidamente". O outro lado da mesma moeda é dividir um número e repetir o processo indefinidamente. Sabemos que dividir qualquer coisa pela metade resulta em partes menores. Repetindo a divisão de novo e de novo iria acabar no nível atômico e depois, subatômico. Porém a matemática nos permite ir além do nível do menor átomo e aí esta a abstração. Como pode algo ser menor do que a menor partícula subatômica?
A definição de um limite quando temos o infinito é fundamentalmente a mesma de calcular o limite para um ponto dado qualquer:
[math]\displaystyle{ 0 \lt |x - a| \lt \delta \implies f(x) \gt M }[/math]
A distância entre dois pontos consecutivos da função é positiva. [math]\displaystyle{ \delta }[/math] é maior do que esta distância.
M é um número grande, o maior que alguém poderia pensar. Estamos afirmando que não importa quão grande M seja, [math]\displaystyle{ f(x) }[/math] ainda assim é maior. Então,
(Se você não conseguiu entender bem o conceito. Tente um número grande como 99 ou 1000. Calcule a função para aquele número. Tente outro número ainda maior e repita. É este o significado do epsilon e delta.)
Agora para os limites laterais:
Se [math]\displaystyle{ f(x) \gt M }[/math] sempre que [math]\displaystyle{ 0 \lt x - a \lt \delta }[/math], escrevemos
[math]\displaystyle{ \lim_{x \ \to \ a^{+}} = +\infty }[/math]
[math]\displaystyle{ \lim_{x \ \to \ a^{-}} = +\infty }[/math]
Se ambos os lados convergirem para o mesmo limite. O limite existe e é o próprio infinito. O outro caso é [math]\displaystyle{ f(x) \lt -M }[/math] para o infinito negativo.
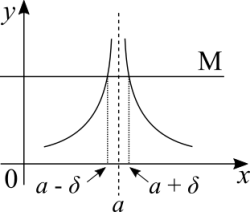
Graficamente temos isto:
Alguém pode perguntar: O gráfico chega a encostar ou ultrapassar a linha tracejada (assíntota)? Podemos imaginar que o gráfico tocará a linha tracejada no infinito, mas em termos práticos isso nunca vai acontecer. É errado escrever [math]\displaystyle{ f(x) = \infty }[/math] porque o infinito nunca pode ser alcançado. O gráfico mostra que M é grande, mas a função ultrapassa este valor. Aqui temos um nível de abstração porque [math]\displaystyle{ a }[/math] é um valor finito na reta dos números, enquanto estamos considerando que lá para cima no infinito a função continua a crescer sem fim. Não existe um "teto" ou borda superior. Para o infinito negativo é o mesmo conceito, exceto que o gráfico vai para baixo, o M é negativo e a função decresce para além de M.
Outra questão pode surgir aqui: o gráfico é simétrico mas o conceito se aplica a qualquer função contínua. A simetria do gráfico é para mostrar que a função tem dois limites, à esquerda e à direita de [math]\displaystyle{ a }[/math] e que ambos convergem para o mesmo ponto. Se a função for [math]\displaystyle{ f(x) = e^x }[/math] por exemplo, o limite existe no infinito mas o gráfico não tem simetria. Neste caso é mais difícil de imaginar porque, assumindo que [math]\displaystyle{ a }[/math] já é um número grande, entre ele e o infinito há números muito grandes e ainda maiores que não seremos capazes de marcar num gráfico à direita de [math]\displaystyle{ a }[/math]. O gráfico existe no infinito, mas não podemos traçá-lo. Algumas pessoas podem achar bem difícil de entender este conceito abstrato, mas para outros pode ser natural.
Limites com infinito
Agora o problema oposto ao anterior, [math]\displaystyle{ x \to \infty }[/math] com a função tendo um limite finito naquele ponto. Este caso pode ser mais fácil de entender porque o limite existe e é um número. Uma borda visível pode ser mais fácil de compreender o limite comparado a um limite que é infinito.
Para todo [math]\displaystyle{ \epsilon \gt 0 }[/math], existe um [math]\displaystyle{ \delta \gt 0 }[/math] tal que [math]\displaystyle{ |f(x) - L| \lt \epsilon }[/math] para todo [math]\displaystyle{ x \gt \delta }[/math].
Em outras palavras: [math]\displaystyle{ \lim_{x \ \to \ \infty} f(x) = L }[/math]
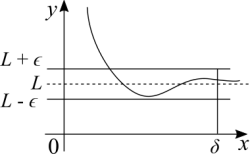
Representação gráfica:
Observação: a linha tracejada significa que, no infinito, o gráfico esta convergindo para aquele valor. [math]\displaystyle{ f(\infty) = L }[/math] não esta certo. Podemos calcular [math]\displaystyle{ f(x) }[/math] para qualquer número muito grande, mas o infinito nunca pode ser alcançado. O que o gráfico mostra é que temos um ponto [math]\displaystyle{ \delta }[/math] onde a função é contínua e o limite existe. Podemos escolher outro número próximo a [math]\displaystyle{ \delta }[/math] indefinidamente. Tal que o limite exista, não é igual ao ponto anterior e a distância [math]\displaystyle{ L - \epsilon \lt f(x) \lt L + \epsilon }[/math] se reduz mais e mais. Esta é a ideia, o processo de encontrar números que são maiores do que o anterior enquanto a distância entre o gráfico da função e o limite esta encolhendo cada vez mais é infinito, nunca termina.
Outra questão pode surgir aqui: e quanto aos limites laterais? Esta pergunta não faz sentido de certa forma e o problema esta em pensar que existe algo à direita do infinito. Pense sobre isto: [math]\displaystyle{ ]\delta, \infty[ }[/math] é um intervalo onde [math]\displaystyle{ \delta }[/math] é um número bem grande. À direita dele há outro número ainda maior e mais outro, sempre há um maior ainda. Há um número à direita do infinito? Primeiro, infinito não é um número. Não pode existir um número à direita do infinito. Segundo, já estamos considerando que [math]\displaystyle{ \delta }[/math] é o maior número que podemos imaginar. Infinito nunca é um ponto ou posição na reta dos números. Porque se marcarmos uma posição com infinito, sempre haverá um ponto ou posição à direita desta.
Alguém pode perguntar: existe um limite que mistura zero com infinito? Pode acontecer de uma conta chegar na forma [math]\displaystyle{ 0/\infty }[/math] ou vice-versa. Para estes casos precisamos comparar o limite problemático com outro que possamos resolver. É o mesmo raciocínio aplicado para resolver integrais impróprias quando não podemos ter certeza se a integral esta ou não convergindo para um certo número ou divergindo para infinito. Porém, temos que ter certeza que não cometemos nenhum erro algébrico em nenhuma conta. É muito raro um exercício de limite ter uma indeterminação na forma de quociente com zero e infinito ao mesmo tempo.
Referência: