Limites e continuidade de funções de várias variáveis

O conceito básico continua o mesmo. Porém, em 2D as coisas mais complicadas do que em 1D. Em 1D você só pode andar para frente ou para trás. Em 2D você pode andar em círculos ao redor de um ponto. O que significa que às vezes o limite pode não existir em uma direção, mas existir na outra. De acordo com o ciclo trigonométrico é razoável imaginar que existam pelo menos 360 caminhos diferentes para se chegar num ponto em 2D.

Para uma variável damos um passo para a esquerda ou para a direita. Para duas variáveis podemos dar um passo para cima ou para baixo, além da esquerda e direita. Para três variáveis podemos dar passos para frente e para trás, além das outras duas direções. Em 2D temos um círculo de pontos ao redor do ponto onde queremos saber se o limite existe ou não. Em 3D uma esfera de pontos.

A ideia dos 360° para funções de duas variáveis é mais ou menos a ideia do "Triângulo de Penrose". A partir de um certo ângulo parece um triângulo completo, mas a partir de outro existe uma quebra na figura. Gere uma função descontínua de duas variáveis num aplicativo e gire a visualização tentando "esconder" a descontinuidade.

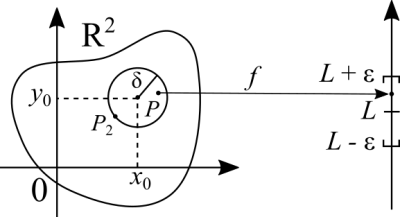
Em 2D temos uma equação de um círculo e em 3D uma esfera. A equação da circunferência é: [math]\displaystyle{ (x - x_0)^2 + (y - y_0)^2 = \delta^2 \iff \delta = \sqrt{(x - x_0)^2 + (y - y_0)^2} }[/math] (não estamos interessados num raio negativo. Podemos ignorar a raiz negativa). A equação também é a distância entre a origem da circunferência e [math]\displaystyle{ P_2 }[/math]. Suponha que [math]\displaystyle{ P = (a,b) }[/math] esta localizado em qualquer ponto do círculo, exceto pelo perímetro. A sua imagem, [math]\displaystyle{ f(P) }[/math] estará localizada em qualquer lugar no intervalo [math]\displaystyle{ \left[L - \epsilon, L + \epsilon\right] }[/math].

Note também como a figura representa graficamente esta propriedade: [math]\displaystyle{ |a - b| = \sqrt{(a - b)^2} }[/math]. A distância não pode ser negativa. Podemos ver as coordenadas dos pontos como vetores de deslocamento. Tanto [math]\displaystyle{ P_2 }[/math] quanto a origem do círculo são pontos que são deslocados da origem do plano cartesiano para as suas respectivas posições mostradas no gráfico (soma de vetor com ponto). Vetorialmente podemos interpretar o raio do círculo assim [math]\displaystyle{ ||\overrightarrow{P_2} - \overrightarrow{C}|| = \delta }[/math], onde [math]\displaystyle{ \overrightarrow{C} }[/math] é o vetor deslocamento da origem do círculo.

A notação é a mesma usada com limites de funções de uma variável:

[math]\displaystyle{ \lim_{(x,\ y) \ \to \ (x_0,\ y_0)} f(x,y) = L }[/math] (para mais de duas variáveis é a mesma coisa)

Para cada [math]\displaystyle{ \epsilon \gt 0 }[/math] há um um [math]\displaystyle{ \delta \gt 0 }[/math], tal que cada [math]\displaystyle{ (x,\ y) \in D_f }[/math], [math]\displaystyle{ 0 \lt \sqrt{(x - x_0)^2 + (y - y_0)^2} \lt \delta \implies |f(x,y) - L| \lt \epsilon }[/math]. (alguns livros substituem a raiz quadrada pela norma e a diferença entre as coordenadas. É a mesma coisa)

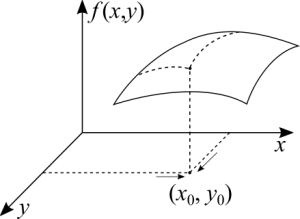
O conceito é virtualmente o mesmo do caso das funções de uma variável. Estamos considerando a menor distância entre dois pontos em 2D que seja o mais próximo possível do zero. Enquanto o erro, a distância entre a imagem e o limite, é o menor valor possível. Note que a definição do limite para várias variáveis não considera o caminho até o ponto. O conceito de limites laterais para várias variáveis é um pouco mais complicado porque em 2D e 3D temos para cima e para baixo, frente e trás e há muito mais lados e direções para serem analisados.

Terminologia: quando um limite existe num ponto [math]\displaystyle{ (x_0, y_0) }[/math], aquele ponto é chamado de ponto limite ou ponto de acumulação. Este termo vem da topologia.

Continuidade: a discussão é exatamente a mesma para uma ou várias variáveis.

[math]\displaystyle{ \lim_{(x,\ y) \ \to \ (x_0,\ y_0)} f(x,\ y) = f(x_0,\ y_0) }[/math]

Se a função é definida em [math]\displaystyle{ (x_0, y_0) }[/math] e o limite converge para aquele ponto, a função é contínua ali. Estenda o mesmo raciocínio para qualquer ponto [math]\displaystyle{ (x, y) }[/math] escolhido do domínio da função e a função é contínua em todo o seu domínio.

Teorema do confronto para várias variáveis

É o mesmo conceito para variáveis de uma variável. Não há diferenças.

Se [math]\displaystyle{ f(x,\ y) \leq g(x,\ y) \leq h(x,\ y) }[/math] for [math]\displaystyle{ 0 \leq \sqrt{(x - x_0)^2 + (y - y_0)^2} \lt \delta }[/math] e

[math]\displaystyle{ \lim_{(x,\ y) \ \to \ (x_0,\ y_0)} f(x,y) = L = \lim_{(x,\ y) \ \to \ (x_0,\ y_0)} h(x,\ y) }[/math]

Então

[math]\displaystyle{ \lim_{(x,\ y) \ \to \ (x_0,\ y_0)} g(x,\ y) = L }[/math]

A mesma propriedade dos limites para uma variável se aplica para várias variáveis. Se uma função limitada é multiplicada por outra, cujo limite vai para zero, podemos dizer que o limite do produto também é zero.

Limites de "múltiplos lados"

É inviável calcular o limite cem vezes só para verificar se ele existe ou não. Precisamos de algo para tratar deste caso. Nós temos uma ferramenta e são as equações paramétricas que descrevem trajetórias. Quando traçamos curvas de nível para funções de duas variáveis temos um caminho e uma equação com duas variáveis, sob a condição especial de que a equação é igual a um nível constante. O que estamos procurando não é exatamente uma função vetorial que descreva uma trajetória no espaço, que no caso seria um caminho sobre a superfície da função de duas variáveis. Nosso problema é que temos um ponto inicial em qualquer lugar no domínio da função, o plano XY ou parte deste, e queremos andar em direção a outro ponto, o ponto que queremos saber se o limite existe ou não. É difícil de imaginar, mas cada passo que dermos em qualquer direção no domínio da função é refletido no gráfico da mesma.

(Observe que temos duas retas sobre o domínio, paralelas à cada eixo, para chegar naquele ponto. Por outro lado, na superfície da função a trajetória não é plana. A menos que a superfície da função seja plana em si)

Quais são os caminhos mais fáceis de verificar? Os mais óbvios são os próprios eixos X e Y. Igualando uma variável a zero reduzimos o limite de duas variáveis para uma só. O próximo caminho é igualando uma variável à outra [math]\displaystyle{ x = y }[/math], o que significar andar sobre a diagonal do plano cartesiano. Um outro caminho muito usado é [math]\displaystyle{ y = x^2 }[/math]. Uma parábola.

Eu tenho um livro que descreve o mesmo conceito de um modo um pouco mais complicado. No lugar de considerar [math]\displaystyle{ x = y }[/math] por exemplo, ele considera uma curva [math]\displaystyle{ \gamma(t) = (x(t), \ y(t)) }[/math]. É uma função de uma variável, neste caso o tempo, que na saída produz posições no plano cartesiano. É por isto que podemos pegar [math]\displaystyle{ f(x,y) }[/math] e escrever [math]\displaystyle{ f(\gamma(t)) }[/math]. Não "apagamos" as duas variáveis. Apenas as "escondemos" numa outra função que traça trajetórias no plano XY. Alguns livros trazem exemplos com a notação assim [math]\displaystyle{ f(t,t^2) }[/math]. É fundamentalmente o mesmo conceito que escrever [math]\displaystyle{ f(x, y=x^2) }[/math].

De certa forma estamos aplicando uma técnica que olha para o problema do limite de uma função de duas variáveis e impõe algumas condições que nos permitem tratar o limite como se fosse um caso de uma função de uma variável. Quando fazemos [math]\displaystyle{ x = 0 }[/math] ou [math]\displaystyle{ y = 0 }[/math] não estamos exatamente transformando uma função de duas variáveis em uma função de uma só. O que estamos fazendo na verdade é "cortando" a função com um plano e olhando a sua "silhueta" deixada pela intersecção da função com o plano. Esta silhueta pode ser interpretada como uma função de uma variável porque é, na realidade, uma linha com espessura nula.

Eu vou mostrar alguns gráficos feitos com o Geogegra 3D para ajudar a ter uma visão melhor sobre os limites de uma função de duas variáveis:

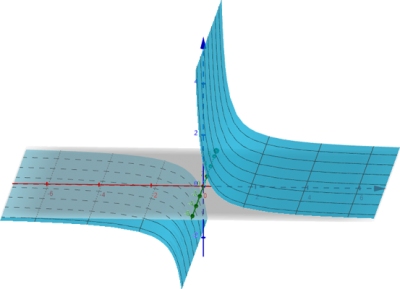
Vamos pegar um caso clássico de função de uma variável [math]\displaystyle{ f(x) = \frac{1}{x} }[/math] e estender para 3D, com a segunda variável mantida constante. Observe que neste caso o comportamento da função é exatamente o mesmo do caso de uma variável. Aproximando-se pela esquerda e pela direita resulta em limites diferentes.

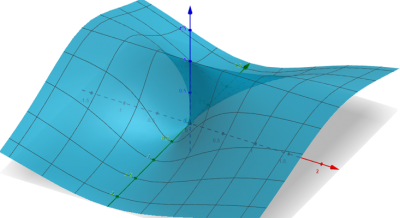
Agora vamos ver o caso de [math]\displaystyle{ f(x,y) = \frac{x^2}{x^2 + y^2} }[/math]. O eixo azul é o Z, o vermelho é o X e o verde é o Y. Observe que se andarmos ao longo dos eixos X e Y, os limites na origem estão em coordenadas Z diferentes. Se andarmos ao longo das diagonais, mais uma altura Z diferente quando nos aproximamos da origem. É impossível para a função ter valores diferentes para um mesmo ponto do seu domínio. O gráfico é renderizado como se fosse uma superfície contínua, mas isto é porque é impossível renderizar com uma resolução infinita. A descontinuidade na origem tem o tamanho de um pixel.

Podemos aplicar o mesmo raciocínio para três ou mais variáveis tranquilamente. Os livros que eu conheço não trazem exercícios de limites para funções de mais do que duas variáveis. Eu suponho que acaba sendo um processo cansativo quando se tem caminhos em 3D e além. Fica impraticável fazer à mão.