Increasing and decreasing functions

At school we learn to identify crescent and decrescent intervals of functions by inspecting their respective graphs. If the teacher explains the rate of change we can have a better understanding of it. Otherwise we are left with the argument that the graph shows the obvious and no further explanations are given. What we don't learn is that a derivative is a tool that we need to prove that the function is crescent or decrescent in a certain interval.

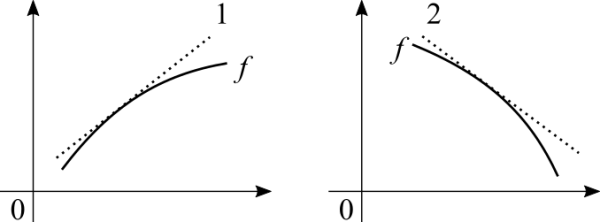
Case 1 the tangent is positive, with a positive rate of change the function is increasing. Case 2 the tangent is negative, with a negative rate of change the function is decreasing. Careful! The above graphs deals with a small closed interval. A function may be always crescent, always decrescent, always constant or display different behaviours at different intervals.

For multivariable functions this concept is a little more complicated. The function may be increasing in one variable but decreasing on the other variable at the same time.

Prove that a function is crescent or decrescent on an interval

If [math]\displaystyle{ f'(x) \gt 0 }[/math] on a interval, then [math]\displaystyle{ f }[/math] is increasing in that interval.

Let [math]\displaystyle{ x_1 }[/math] and [math]\displaystyle{ x_2 }[/math] be two numbers in the interval with [math]\displaystyle{ x_1 \lt x_2 }[/math]. For a function to be increasing we have to show that [math]\displaystyle{ f(x_1) \lt f(x_2) }[/math]. Because we are given that [math]\displaystyle{ f'(x) \gt 0 }[/math], we know that [math]\displaystyle{ f }[/math] is differentiable on [math]\displaystyle{ [x_1, \ x_2] }[/math]. We are assuming the function to be differentiable, else we could not do the proof.

Now the Mean Value Theorem states that between [math]\displaystyle{ x_1 }[/math] and [math]\displaystyle{ x_2 }[/math] there is going to be a [math]\displaystyle{ c }[/math] such that the derivative is equal to the average rate of change between the latter two points. We are trying to prove that the function is crescent in that interval, which translates into assuming that the derivative is always positive in that interval. Never assuming negative values or the zero, which would mean that in that interval the function inverts its rate of change. Something that can't happen if we already began the proof by saying that [math]\displaystyle{ f'(x) \gt 0 }[/math]. Applying the MVT:

[math]\displaystyle{ f(x_2) - f(x_1) = f'(c)(x_2 - x_1) }[/math]

We know that [math]\displaystyle{ x_2 - x_1 \gt 0 }[/math] because [math]\displaystyle{ x_2 \gt x_1 }[/math]. Thus the right side of the equation is positive, and so

[math]\displaystyle{ f(x_2) - f(x_1) \gt 0 \iff f(x_2) \gt f(x_1) }[/math]

That proves that [math]\displaystyle{ f }[/math] is increasing.

If [math]\displaystyle{ f'(x) \lt 0 }[/math] on a interval, then [math]\displaystyle{ f }[/math] is decreasing in that interval.

We can go on with the same reasoning as before:

[math]\displaystyle{ f(x_2) - f(x_1) = f'(c)(x_2 - x_1) }[/math]

We know that [math]\displaystyle{ x_2 - x_1 \gt 0 }[/math] because [math]\displaystyle{ x_2 \gt x_1 }[/math]. Thus both sides of the equation are negative (we began with the assumption that [math]\displaystyle{ f'(x) \lt 0 }[/math], which implies that the left side is also negative), and so:

[math]\displaystyle{ f(x_2) - f(x_1) \lt 0 \iff f(x_2) \lt f(x_1) }[/math]

That proves that [math]\displaystyle{ f }[/math] is decreasing.