Funções crescentes e decrescentes

Na escola aprendemos a identificar intervalos de funções que sejam crescentes ou decrescentes por uma inspeção do seu gráfico. Se o professor explicar taxas de variação temos uma melhor compreensão. Caso contrário ficamos com o argumento de que o gráfico mostra o óbvio sem maiores explicações. O que não aprendemos é que a derivada é uma ferramenta necessária para provar que uma função é crescente ou decrescente num certo intervalo.

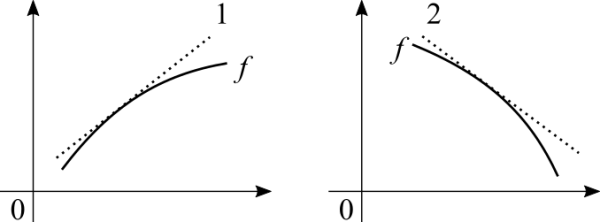
Caso 1 a tangente é positiva. Com uma taxa de variação positiva a função é crescente. Caso 2 a tangente é negativa. Com uma taxa de variação negativa a função é decrescente. Cuidado! O gráfico acima só aborda um pequeno intervalo fechado. Uma função pode ser sempre crescente, sempre decrescente, sempre constante ou se comportar de maneira diferente em diferentes intervalos.

Para funções de várias variáveis este conceito é um pouco mais complicado. A função pode crescer numa variável mas decrescer na outra ao mesmo tempo.

Prove que uma função é crescente ou decrescente num intervalo

Se [math]\displaystyle{ f'(x) \gt 0 }[/math] num intervalo, então [math]\displaystyle{ f }[/math] é crescente naquele intervalo.

Sejam [math]\displaystyle{ x_1 }[/math] e [math]\displaystyle{ x_2 }[/math] dois números no intervalo com [math]\displaystyle{ x_1 \lt x_2 }[/math]. Para uma função ser crescente temos que mostrar que [math]\displaystyle{ f(x_1) \lt f(x_2) }[/math]. Como temos [math]\displaystyle{ f'(x) \gt 0 }[/math], sabemos que [math]\displaystyle{ f }[/math] é diferenciável em [math]\displaystyle{ [x_1, \ x_2] }[/math]. Estamos assumindo que a função seja diferenciável, senão não podemos provar o que queremos.

O Teorema do Valor Médio afirma que entre [math]\displaystyle{ x_1 }[/math] e [math]\displaystyle{ x_2 }[/math] existe um [math]\displaystyle{ c }[/math] tal que a derivada é igual à taxa de variação média entre os dois pontos citados anteriormente. Estamos tentando provar que a função é crescente naquele intervalo, o que se traduz em assumir que a derivada é sempre positiva no intervalo. Ela nunca é negativa ou nula, o que implicaria que no intervalo a função inverteria a sua taxa de variação. Estas últimas possibilidades estão eliminadas no momento em que começamos a demonstração dizendo que [math]\displaystyle{ f'(x) \gt 0 }[/math]. Aplicando o TVM:

[math]\displaystyle{ f(x_2) - f(x_1) = f'(c)(x_2 - x_1) }[/math]

Sabemos que [math]\displaystyle{ x_2 - x_1 \gt 0 }[/math] porque [math]\displaystyle{ x_2 \gt x_1 }[/math]. Ou seja, o lado direito da equação é positivo. Daí:

[math]\displaystyle{ f(x_2) - f(x_1) \gt 0 \iff f(x_2) \gt f(x_1) }[/math]

Isto prova que [math]\displaystyle{ f }[/math] é crescente.

Se [math]\displaystyle{ f'(x) \lt 0 }[/math] num intervalo, então [math]\displaystyle{ f }[/math] é decrescente naquele intervalo.

Podemos seguir o mesmo raciocínio anterior:

[math]\displaystyle{ f(x_2) - f(x_1) = f'(c)(x_2 - x_1) }[/math]

Sabemos que [math]\displaystyle{ x_2 - x_1 \gt 0 }[/math] porque [math]\displaystyle{ x_2 \gt x_1 }[/math]. Ou seja, ambos os lados da equação são negativos (começamos assumindo que [math]\displaystyle{ f'(x) \lt 0 }[/math], o que implica que o lado esquerdo também é negativo). Daí:

[math]\displaystyle{ f(x_2) - f(x_1) \lt 0 \iff f(x_2) \lt f(x_1) }[/math]

Isto prova que [math]\displaystyle{ f }[/math] é decrescente.