Examples of level surfaces

It's really easy to confuse the level surface of a function of three variables with the graph of a function of two variables! Careful here! In 3D we can have the axis in any order that we want. For this type of exercise we aren't concerned with what process that function is associated to. Our only concern here is with "what side is up?". The level surfaces were hand drawn in inkscape with no scale at all.

[math]\displaystyle{ f(x,y,z) = x + 3y + 5z }[/math]	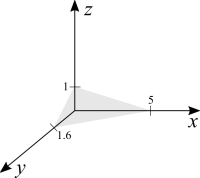Make the function equal to a constant and we have [math]\displaystyle{ c = x + 3y + 5z }[/math]. For infinitely many points [math]\displaystyle{ (x,y,z) }[/math] we have the same value for the function. If you know the equation of a plane from analytical geometry you'll quickly notice that we have an equation of a plane here. Now to plot the plane it's impractical to get the right angle and perspective in 3D by hand. What we can do is to rely on the points where the plane intersects the axes. Let's choose [math]\displaystyle{ c = 5 }[/math]. [math]\displaystyle{ 5 = 5 + 0 + 0 }[/math]. It intersects the first axis at [math]\displaystyle{ x = 5 }[/math] [math]\displaystyle{ 5 = 0 + 3y + 0 }[/math]. It intersects the second axis at [math]\displaystyle{ y = 5/3 }[/math] [math]\displaystyle{ 5 = 0 + 0 + 5z }[/math]. It intersects the third axis at [math]\displaystyle{ z = 1 }[/math] For this exercise we don't need to have perfect proportions, round up/down the decimals and it should be OK.
[math]\displaystyle{ f(x,y,z) = x^2 + y^2 + z^2 }[/math]	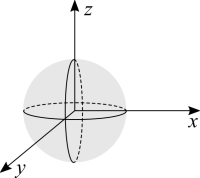The correct way to view this is to think in terms of the equation for the distance between points from analytical geometry. In the same way that [math]\displaystyle{ c = x^2 + y^2 }[/math] finds all points for a circle of radius equal to [math]\displaystyle{ c }[/math]. Adding the term [math]\displaystyle{ z^2 }[/math] finds all points in 3D space that have a constant distance from the origin. That's a sphere. Multiply the variables by a constant and we effectively deform the sphere, transforming it into a ellipsoid.
[math]\displaystyle{ f(x,y,z) = y^2 + z^2 }[/math]	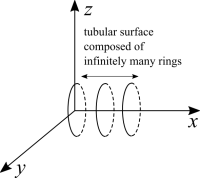The first impression may be of a paraboloid, but it's not. In the same way a level curve of that form for a function of two variables is a circle. We have the equation of a circle [math]\displaystyle{ c = y^2 + z^2 }[/math], except that rather than a circle on the XY plane, it's a circle on the YZ plane. With infinitely many circles in front (or on top, depending on your viewpoint) of each other, what shape do we have? A tube, or a cylinder. Remember that there is a "hidden" [math]\displaystyle{ 0x }[/math] in the function's equation.
[math]\displaystyle{ f(x,y,z) = x^2 - y^2 - z^2 }[/math]	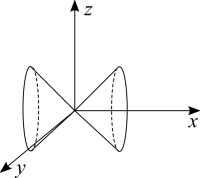The first impression may be of a sphere, but it's not. The minus sign makes a huge difference! One way to analyse the shape is by looking at the XY, XZ, YZ planes. Disregard one of the variables and look at the remaining two. Looking at XY or XZ and we see the level curves of a paraboloid, hyperboles. YZ seems to be a paraboloid flipped upside down, the level curves are circles. In analytical geometry we obtain hyperboles, circles and ellipsis by slicing a cone with planes. This should give us the idea the the level surfaces of this function is a cone. Now if we isolate one variable, we find some interesting shape. [math]\displaystyle{ z = \pm \sqrt{x^2 + y^2} }[/math], it's the equation of a cone. It's mirrored in both directions because of the [math]\displaystyle{ z^2 }[/math] term. Changing the plus sign from one variable to another essentially rotates the cone in space.
[math]\displaystyle{ f(x,y,z) = x }[/math]	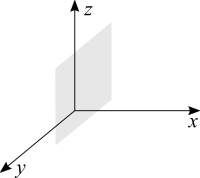The idea is very similar to a function of two variables with one of the variables missing from the equation. [math]\displaystyle{ f(x,y) = x }[/math] produces a plane, but it has a slope because its "height" is not constant. Its level curves are all parallel lines. Going to 3D and we have parallel flat level surfaces. The question is: planes oriented which way? Which way is up? Let's choose [math]\displaystyle{ c = 1 }[/math]. Now let's take a look at which triplets can satisfy that level: [math]\displaystyle{ (1,y,z) }[/math]. The first coordinate is fixed, the other two can have any number from negative, to zero to positive. Remember, they are there in the form of [math]\displaystyle{ 0y + 0z }[/math]. They all map to the same level. The standard XYZ view that every book has is with [math]\displaystyle{ x }[/math] being the horizontal axis, [math]\displaystyle{ z }[/math] the vertical axis and [math]\displaystyle{ y }[/math] the axis that represents "depth", "inside" and "outside" the paper or the computer's screen. With that in mind, our surface level is a plane that is parallel to the ZY plane, perpendicular to X. Anywhere we walk over that surface has a fixed X coordinate while Y and Z are free.