[math]\displaystyle{ f(x,y) = x^2 + y^2 }[/math]
 |
Make the function equal to a constant [math]\displaystyle{ f(x,y) = 1 }[/math]. Then [math]\displaystyle{ 1 = x^2 + y^2 }[/math]. If you know the equation of a circle it should be obvious that this is the equation of a circle with radius = 1. Choose [math]\displaystyle{ x = 0 }[/math] and you get [math]\displaystyle{ y = \pm \sqrt{1} }[/math]. Repeat for [math]\displaystyle{ y = 0 }[/math] and you get [math]\displaystyle{ x = \pm \sqrt{1} }[/math]. This should give four points on the XY plane. How do we know that the points are connected with a circle and not a square diamond? Because the equation is not linear, it has squares on it. The circles being symmetric in both axes explain why the function is symmetric in both axes. Multiply one variable by a constant and we effectively deform the circles, making them ellipsis.
The other way to picture the level curve is by isolating either [math]\displaystyle{ x }[/math] or [math]\displaystyle{ y }[/math] to get a function of one variable, such as [math]\displaystyle{ y = \pm \sqrt{1 - x^2} }[/math] which translates to [math]\displaystyle{ f(x) = \sqrt{1 - x^2} }[/math] or [math]\displaystyle{ f(x) = -\sqrt{1 - x^2} }[/math].
There is a little mistake that can happen regarding the circle's radius. Pay attention to the square. I plotted the levels 4 and 9 because the radius is squared. So for the level 4, [math]\displaystyle{ x = 2^2 }[/math]. The level 2 would had been [math]\displaystyle{ x = \sqrt{2}^2 }[/math] which is hard to get the right distance without having a scale to measure.
For [math]\displaystyle{ e^{-x^2 - y^2} }[/math] and [math]\displaystyle{ \sin(x^2 + y^2) }[/math] the level curves are circles too. Except that the levels have different meanings. For the exp, we have the levels [math]\displaystyle{ e^0, \ e^1, \ e^2, \ ... }[/math]. For the sine, it's the angle [math]\displaystyle{ \theta_1, \ \theta_2, \ \theta_3, \ ... }[/math]
|
[math]\displaystyle{ f(x,y) = \sin(x + y) }[/math]
 |
The first confusion to avoid is that [math]\displaystyle{ \sin(x) }[/math] is not a linear function, but [math]\displaystyle{ x + y }[/math] is linear. The level curves are going to be straight lines, not waves. For each [math]\displaystyle{ \theta }[/math] there are infinitely many pairs [math]\displaystyle{ (x,y) }[/math] that add up to that angle. For example: [math]\displaystyle{ \pi/4 = 0 + \pi/4 }[/math] or [math]\displaystyle{ \pi/4 = \pi/4 + 0 }[/math]. Repeat for other angles to plot more level curves.
The second mistake is that the function is non-linear, which means that the distance between level curves cannot be a constant. If we take increments at a constant rate, such as [math]\displaystyle{ \pi/2 }[/math] we do see evenly spaced level curves. However, in between [math]\displaystyle{ 0 }[/math] and [math]\displaystyle{ \pi/2 }[/math] we have the angles [math]\displaystyle{ \pi/4 }[/math] and [math]\displaystyle{ \pi/6 }[/math] and the distance between them is no longer constant.
|
[math]\displaystyle{ f(x,y) = x/y }[/math]
 |
Again, the function is non-linear, yet the level curves are straight lines. [math]\displaystyle{ c = x/y \iff y = x/c }[/math], that's the equation of a line where [math]\displaystyle{ c }[/math] changes the slope of it. The function is undefined for [math]\displaystyle{ (x, 0) }[/math] (all points over the [math]\displaystyle{ x }[/math] axis) or [math]\displaystyle{ (0,0) }[/math]. It's a bit hard to picture it, but try to imagine twisting a sheet of paper. One side is twisted clockwise. The opposite side is twisted anti-clockwise. For each level the curves are "rotating" with a maximum angle of < 360°. Going above that would make the function intersect itself.
For [math]\displaystyle{ c = 1 }[/math], we have [math]\displaystyle{ x = y }[/math]
For [math]\displaystyle{ c = 2 }[/math], we have [math]\displaystyle{ x/2 = y }[/math]
For [math]\displaystyle{ c = 3 }[/math], we have [math]\displaystyle{ x/3 = y }[/math]
So on
Note: if you plot this graph on google or wolfram, you'll notice that there is a gap in the function when viewed from above and some parabolas at certain angles. It's an illusion. If [math]\displaystyle{ c \ \to \ \pm \infty }[/math] the slope of a level curve goes to zero. The curvature that you see is caused by the fact that the relationship [math]\displaystyle{ x/y }[/math] is not constant.
|
[math]\displaystyle{ f(x,y) = x^2 - y^2 }[/math]
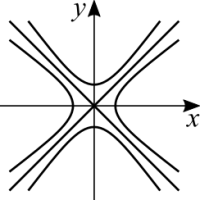 |
By inverting the sign of one of the parabolas, what was a paraboloid is now a hyperbolic paraboloid. If you know the equation of hyperbolas it's going to be quick to notice that the level curves are hyperbolas. When [math]\displaystyle{ f(x,y) = 0 \ ? }[/math] When [math]\displaystyle{ x^2 = y^2 }[/math], which is the same as [math]\displaystyle{ x = y }[/math]. We have two level curves with this reasoning, both the diagonals of the XY plane. Along the diagonals the function is null.
[math]\displaystyle{ 1 = 0^2 + y^2 }[/math]. With this we have that when [math]\displaystyle{ x = 0 }[/math], [math]\displaystyle{ y = \pm 1 }[/math]. This shows us that the hyperbola is not going to cross the origin.
[math]\displaystyle{ 1 = x^2 + 0^2 }[/math]. The same reasoning for the other variable and we find another hyperbola on the other direction.
[math]\displaystyle{ c + x^2 = y^2 \iff y = \pm \sqrt{c + x^2} }[/math]. This resembles the equation of a a function that plots half a circle, except that the minus sign is now a plus sign. It's easy to notice that the change on the sign makes each point go farther and farther away from the origin rather than keeping a constant distant from it.
|
[math]\displaystyle{ f(x,y) = \sin(|x| + |y|) }[/math]
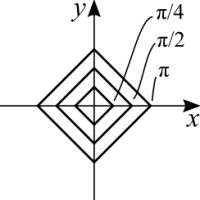 |
Just by glancing at it and we can already assume that the level curves are straight lines. However, there is the absolute value now. For positive coordinates the level curve is exactly the same as [math]\displaystyle{ \sin(x + y) }[/math]. What happens when one or both are negative? [math]\displaystyle{ \theta = |x| + |y| }[/math]. Remember, we are not plotting functions. We are asking "What pairs [math]\displaystyle{ (x,y) }[/math] satisfy that angle?".
Suppose the constant is [math]\displaystyle{ \pi }[/math]. Which pairs do we have that add up to that angle? [math]\displaystyle{ (\pi, 0) }[/math] and [math]\displaystyle{ (0, \pi) }[/math] we already know from the previous example. With the modulus we have two more: [math]\displaystyle{ (-\pi, 0) }[/math] and [math]\displaystyle{ (0, -\pi) }[/math]. From [math]\displaystyle{ \sin(x + y) }[/math] we already know that the level curves are straight lines. With this we can trace level curves that resemble square diamonds.
The graph of this function propagates, symmetrically, in all directions. The shape of the graph is different from [math]\displaystyle{ \sin(x^2 + y^2) }[/math] but notice how the modulus and calculating the square have the same effect of negating negative values for the function. Both functions always stay above zero.
|
[math]\displaystyle{ f(x,y) = xy }[/math]
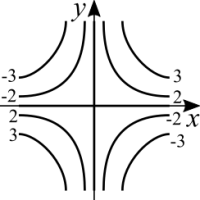 |
Doing [math]\displaystyle{ c = xy }[/math] leads us to a quick conclusion. To keep the level curve at a constant level, [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] must be one the inverse of the other. This reminds us of the single variable function [math]\displaystyle{ f(x) = 1/x }[/math]. Careful with the proportion of the curves! Don't trace perfectly round curves nor curves that are perfectly parallel to each other.
For [math]\displaystyle{ c = 2 }[/math] we have the pairs [math]\displaystyle{ (1,2) }[/math] and [math]\displaystyle{ (2,1) }[/math] (as well as infinitely many others). But there are two more [math]\displaystyle{ (-1,-2) }[/math] and [math]\displaystyle{ (-2,-1) }[/math]. For [math]\displaystyle{ c = -2 }[/math] there are also four possible pairs that satisfy it. Which means that this function has symmetric level curves in all directions. The function also intersects both axis, because when [math]\displaystyle{ x = 0 }[/math] and/or [math]\displaystyle{ y = 0 }[/math], the function is null.
Pay attention to the signs! The function is going up at the 1st and 3rd quadrants and going down at the 2nd and 4th quadrants.
|
[math]\displaystyle{ f(x,y) = \frac{x}{x^2 \ + \ y^2} }[/math]
 |
The denominator being [math]\displaystyle{ x^2 + y^2 }[/math] does make us think on circles. However, the numerator is not a constant, which makes the analysis more complicated. The easiest level curve is when [math]\displaystyle{ x = 0 }[/math] because then the function is zero too.
For [math]\displaystyle{ f(x,y) = c }[/math], we have [math]\displaystyle{ \frac{x}{x^2 + y^2} = c }[/math].
Then [math]\displaystyle{ x = c(x^2 + y^2) }[/math] (Remember that [math]\displaystyle{ x^2 + y^2 \neq 0 }[/math])
Then [math]\displaystyle{ 0 = cx^2 - x + cy^2 }[/math] (we subtracted [math]\displaystyle{ x }[/math] from both sides. It's not the same as making the radius of the circle zero)
Then [math]\displaystyle{ 0 = cx^2 - x + cy^2 }[/math]
Then [math]\displaystyle{ 0 = x^2 - x/c + y^2 }[/math] (we aren't considering the zero constant because we already know the zero level curve and the function is undefined for (0,0))
Then [math]\displaystyle{ 0 = (x - \frac{1}{2c}^2 + \frac{1}{4c^2}+ y^2 \iff \frac{1}{4c^2} = (x - \frac{1}{2c}^2 + y^2 }[/math] (If you noticed, the term [math]\displaystyle{ x^2 - xc }[/math] is an incomplete square. That means that we can complete the squares to rewrite the equation in a form that relates the constant, the function's level, to the radius of the circle)
From that we can see that the constant is part of both the circle's radius and the [math]\displaystyle{ x }[/math] coordinate for its origin. As we calculate the level curve for [math]\displaystyle{ c }[/math], the circle changes its radius as well as its position along the horizontal axis. Now we have to take advantage of limits and see what happens when [math]\displaystyle{ c \to \pm \infty }[/math]. In both cases the radius and the horizontal displacement go to zero, the circle tends to a dot at the origin. For both very large and very negative constants we have even larger radius, while at the same time the circle's origin moves to the right or to the left. We have this symmetry: "o|o" with a circle never crossing the [math]\displaystyle{ y }[/math] axis.
There is one mistake that can happen here because of the minus sign. All the previous analysis lead to us to view two symmetric level curves in the shape of circles. Which way is left and which way is right? When we have this form [math]\displaystyle{ (x - a)^2 }[/math], for [math]\displaystyle{ a \gt 0 }[/math] the circle is moving to the right. For [math]\displaystyle{ a \lt 0 }[/math] the circle is moving to the left. This function increases when we approach the origin from any point located to the right of the [math]\displaystyle{ y }[/math] axis and decreases from any point located to the left of the [math]\displaystyle{ y }[/math] axis. Going away from the origin in any direction and the function is going to zero because of the term [math]\displaystyle{ 1/(x^2 + y^2) }[/math].
An alternate analysis:
[math]\displaystyle{ y^2 = \frac{x - cx^2}{c} }[/math]
[math]\displaystyle{ y = \pm \sqrt{x/c - x^2} }[/math] (This equation does resemble the function that traces half a circle, except that the radius is non-constant. For every increment of the radius, the graph is also displaced to the right. We could complete the squares in the same way as before.)
|