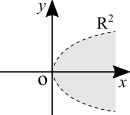
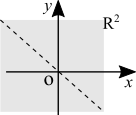
Examples of domain of a multivariable function
From Applied Science
Domain of functions of three variables
| [math]\displaystyle{ f(x,y,z) = \sqrt{1 - x^2 - y^2 - z^2} }[/math] | The domain is [math]\displaystyle{ x^2 + y^2 + z^2 \geq 1 }[/math]. We have a sphere of radius 1 and the domain is all points outside the sphere, including its surface. Points inside the sphere result in a complex number. |
| [math]\displaystyle{ f(x,y,z) = \sqrt{1 - z} }[/math] | The domain is all [math]\displaystyle{ z \leq 1 }[/math] because any [math]\displaystyle{ z \gt 1 }[/math] results in a complex number. The other two variables are free, which means that the domain is all the space under the plane [math]\displaystyle{ z = 1 }[/math], including the plane itself. |
| [math]\displaystyle{ f(x,y,z) = \sqrt{1 - x - y - z} }[/math] for all [math]\displaystyle{ x \geq 0, y \geq 0, z \geq 0 }[/math] |
For the condition given we know that this function's domain is limited between 1 and 0 in all directions. The domain is a prism with some edges equal to 1 and other edges equal to [math]\displaystyle{ \sqrt{2} }[/math]. It's hard to picture it, but the square root cannot be negative. The lowest number is zero. The sum of the three variables can't be greater than 1, making 1 the upper bound. |
| [math]\displaystyle{ f(x,y,z) = \sqrt{1 - |x| - |y| - |z|} }[/math] | This is slightly more complicated than the previous. Disregard two variables, the remaining variable can be anything between 1 and -1. With this reasoning the variables are all limited between 1 and -1. Now on the XY plane, if we connect [math]\displaystyle{ (0,1) }[/math] to [math]\displaystyle{ (1,0) }[/math] we have a triangle. Repeat for the XZ and YZ planes and we have more triangles. Repeat for negative coordinates. The domain of this function resembles an icosahedron. It's hard to plot it without a computer. |