Encontrando pontos críticos de uma função de uma variável
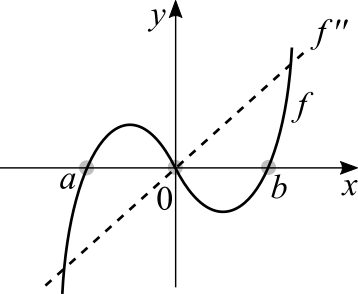
Esta parte continua a discussão de máximos e mínimos de uma função de uma variável. Agora tratamos do caso específico de [math]\displaystyle{ f''(x) = 0 }[/math]. Da mesma forma que a derivada nos motra se uma função é crescente ou decrescente num certo intervalo, a segunda derivada nos diz o mesmo a respeito da própria derivada. Com a derivada segunda sabemos se a taxa de variação da função cresce ou decresce com o tempo. O que graficamente significa que a concavidade do gráfico (sua curvatura) é para cima ou para baixo. Vamos inspecionar o gráfico de uma cúbica e a sua derivada segunda:
[math]\displaystyle{ ]a, \ 0[ }[/math] temos que [math]\displaystyle{ f''(x) \lt 0 }[/math]. A derivada segunda é crescente, o seu sinal é negativo e o gráfico de [math]\displaystyle{ f }[/math] é uma parábola para baixo.
[math]\displaystyle{ ]0, \ b[ }[/math] temos que [math]\displaystyle{ f''(x) \gt 0 }[/math]. A derivada segunda é crescente, o seu sinal é positivo o gráfico de [math]\displaystyle{ f }[/math] é uma parábola para cima.
Na origem [math]\displaystyle{ f''(x) = 0 }[/math]. Quando [math]\displaystyle{ f'(x) = 0 }[/math] isto significa que temos uma tangente horizontal naquele ponto. Quando [math]\displaystyle{ f''(x) = 0 }[/math] isto significa que a derivada mudou de positiva para negativa ou vice-versa. É chamado de ponto de inflexão. Alguns exercícios tentam nos enganar porque aquele ponto pode ter a derivada mudando de crescente para decrescente, o que não é o mesmo comportamento que mudar o seu sinal! Isto ocorre com polinomiais de grau 4 ou maior por exemplo.
A concavidade da função nos conta se a função esta crescendo | decrescendo mais rápido ou mais devagar com o tempo. Se a concavidade for para cima e a função é crescente naquele intervalo, a taxa de variação aumenta com o tempo. Se for para baixo e a função é decrescente naquele intervalo, a taxa de variação diminui com o tempo. Note que quando temos a concavidade para cima ou para baixo num certo intervalo não podem haver pontos de inflexão no mesmo.
Cuidado! Da mesma forma que [math]\displaystyle{ f'(x) = 0 }[/math] é uma condição necessária mas insuficiente para um ponto ser um máximo ou mínimo local. [math]\displaystyle{ f''(x) = 0 }[/math] é uma condição necessária mas insuficiente para um ponto ser de inflexão.
Se [math]\displaystyle{ f }[/math] for duas vezes diferenciável num intervalo aberto [math]\displaystyle{ I }[/math], então:
[math]\displaystyle{ f''(x) \gt 0 }[/math] em [math]\displaystyle{ I }[/math] significa que a concavidade de [math]\displaystyle{ f }[/math] é para cima naquele intervalo.
[math]\displaystyle{ f''(x) \lt 0 }[/math] em [math]\displaystyle{ I }[/math] significa que a concavidade de [math]\displaystyle{ f }[/math] é para baixo naquele intervalo.
(já estamos excluindo funções lineares, porque a derivada de uma função linear sempre é uma constante)
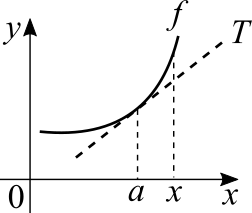
A ideia gráfica da demonstração é bastante simples. Temos que usar o Teorema do Valor Médio e a aproximação linear. Quando a concavidade é para cima, a reta tangente esta abaixo da função. Quando a concavidade é para baixo, a reta tangente esta acima da função. Em outras palavras, o que temos que provar é que a função esta acima da sua aproximação linear se a concavidade for para baixo. Senão, a concavidade é para cima e a função esta acima da sua aproximação linear. Eu vou seguir o livro do Stewart e provar a primeira metade.
Seja [math]\displaystyle{ a }[/math] um número que pertence ao intervalo [math]\displaystyle{ I }[/math]. Precisamos mostrar que [math]\displaystyle{ f(x) \gt T(x) }[/math], onde [math]\displaystyle{ T(x) = f(a) - f'(a)(x - a) }[/math] para todo [math]\displaystyle{ x \in I }[/math], exceto pela intersecção onde [math]\displaystyle{ f(x) = T(x) }[/math].
Se [math]\displaystyle{ x \gt a }[/math], aplicando o Teorema do Valor Médio à [math]\displaystyle{ f }[/math] no intervalo [math]\displaystyle{ [a, \ x] }[/math], obtemos um número [math]\displaystyle{ c }[/math], com [math]\displaystyle{ a \lt c \lt x }[/math], tal que
[math]\displaystyle{ f(x) - f(a) = f'(c)(x - a) }[/math]
Como [math]\displaystyle{ f'' \gt 0 }[/math] em [math]\displaystyle{ I }[/math] sabemos que [math]\displaystyle{ f' }[/math] é crescente em [math]\displaystyle{ I }[/math]. Ou seja, como [math]\displaystyle{ a \lt c }[/math], temos
[math]\displaystyle{ f'(a) \lt f'(c) }[/math]
(para entender porque isto é verdadeiro olhe para o gráfico e preste atenção ao fato de que [math]\displaystyle{ c }[/math] esta em algum lugar depois de [math]\displaystyle{ a }[/math] e antes de [math]\displaystyle{ x }[/math])
Sabemos que [math]\displaystyle{ x - a \gt 0 }[/math], portanto se multiplicarmos ambos os lados um número positivo a inequação não se altera
[math]\displaystyle{ (x - a)f'(a) \lt f'(c)(x - a) }[/math]
Somando o mesmo número a ambos os lados deve manter a inequação verdadeira
[math]\displaystyle{ f(a) + (x - a)f'(a) \lt f'(c)(x -a) + f(a) }[/math]
Olhando para trás podemos substituir o lado direito da equação por [math]\displaystyle{ f(x) }[/math], o que resulta em
[math]\displaystyle{ f(x) \gt f(a) + (x - a)f'(a) }[/math]
que é o resultado que queríamos provar. Com um raciocínio semelhante repetimos o processo para o caso de [math]\displaystyle{ x \lt a }[/math]. Cuidado que na próxima vez temos que [math]\displaystyle{ x - a \lt 0 }[/math].
Eu tenho um livro que faz a demonstração de um modo um pouco diferente. Ele considera a diferença entre a função e a sua aproximação linear. Se a aproximação linear estiver abaixo da função, então temos que provar que a diferença é positiva. Senão, com a aproximação linear acima da função, temos que provar que a diferença é negativa.
Observação: por analogia alguém pode pensar que podemos usar a derivada terceira para saber se o ponto onde [math]\displaystyle{ f''(x) = 0 }[/math] é de inflexão ou não, por comparação com o que fazemos com os máximos e mínimos locais. Não é o caso porque um ponto de inflexão não pode coincidir com um máximo ou mínimo. Por definição temos um ponto onde a concavidade muda de sentido. Na geometria euclidiana padrão é impossível para este ponto ser um máximo ou um mínimo (Eu não tenho ideia se existe uma geometria não euclidiana onde isto é possível).
A informação que poderíamos tirar da derivada terceira seria achar um ponto onde a derivada muda de crescente para decrescente ou vice-versa, o que pode ou não coincidir com um máximo ou mínimo local da própria derivada.