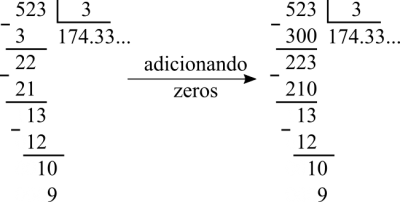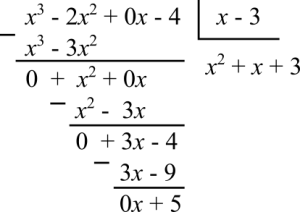Divisão longa de polinômios

Na escola todos são ensinados como dividir um número por outro seguindo o algoritmo a seguir. O primeiro número é chamado de dividendo o segundo de divisor:

É possível que algumas pessoas invertam a ordem, fazendo da direita para a esquerda. Eu não faço ideia da causa, mas eu me lembro de ter confundido isto e mais de uma vez. Estaria relacionado com línguas escritas da direita para a esquerda? Não sei. Se você olhar de outra forma, este algoritmo nada mais é do que: 3 x 100 = 300, depois 523 - 300 = 223. Depois 3 x 70 = 210 e 100 + 70 = 170. Repita. É tudo na base 10. O que fazemos é quebrar um número na base 10, tal como 523 = 500 + 20 + 3. Algumas pessoas possivelmente fazem ao contrário, 3 + 20 + 500 = 523. Agora quanto à vantagem ou desvantagem, é como perguntar se é mais fácil somar de 1 a 10 ou de 10 a 1. Para um computador tanto faz.

Divisão longa de polinômios

Essencialmente é a mesma coisa que dividir números:

O resultado é: [math]\displaystyle{ (x - 3)(x^2 + x + 3) + 5 }[/math]. O erro mais comum aqui é confundir as potências com os coeficientes, como o cubo com a constante 3. O outro é dividir os termos errados. Dividimos term por termo, a potência mais alta pela potência mais alta da mesma forma que dividimos 523 por 3 anteriormente. 5 por 3 dá 1, porque 1 vezes 3 é máximo que podemos ir sem passar de 5. Depois a diferença 5 menos 3 dá 2. Dividimos [math]\displaystyle{ \frac{x^3}{x} = x^2 }[/math], depois [math]\displaystyle{ x^2(x - 3) = x^3 - 3x^2 }[/math]. O próximo erro que costuma ocorrer é que dividimos [math]\displaystyle{ \frac{x^3}{x} }[/math], mas multiplicamos [math]\displaystyle{ x^2(x - 3) }[/math], não apenas [math]\displaystyle{ (x^2)(x) }[/math].

O artigo da wikipedia esta um pouco confuso porque o divisor [math]\displaystyle{ x - 3 }[/math] foi escrito à esquerda e o quociente esta acima do dividendo. Talvez algumas pessoas achem mais fácil ler deste jeito. Eu não sei dizer.