Defining the gradient
To properly understand the gradient one is required to know vectors and the dot (or scalar) product. When we have color gradients what we see is that one extreme has one color and the other extreme another color, in between a gradient that is the transition between one color to the other. In physics there exists many types of gradients, such as gradients of temperature or pressure. Gradients are important because there are certain phenomena that require strong gradients to happen, such as there is no wind or oceanic currents if there is no pressure gradient between two points. Conceptually we have some quantity that changes in intensity over space and with a particular direction. That's the gradient.
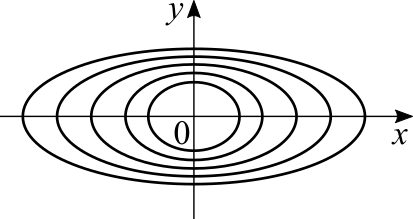
Before going on for a mathematical definition, let's look at a graph of level curves:
The rate of change over the [math]\displaystyle{ x }[/math] axis is less than over the [math]\displaystyle{ y }[/math] axis because the level curves are closer in the latter direction than on the former. If we walk along the same level we don't experience any changes in the value of [math]\displaystyle{ f(x,y) }[/math], which means that the rate of change is zero for directions parallel to a level curve. The highest rates of change are achieved when we move perpendicularly to the level curves, which is the shortest path between them. If the distance between two consecutive level curves is close to zero, it means that the function's slope is close to 90°. Otherwise, if the distance between them tends to infinity, then the slope is close to 0°.
[math]\displaystyle{ D_xf \cdot a + D_yf \cdot b }[/math]. Taking a second look at the directional derivative notice that we have a sum of terms where each one is a product between the coordinates of the vector given and the partial derivatives for that coordinate. That formula is a dot product. Conclusion? We have two vectors in it, one is the vector that gives the direction which we want to find the rate of change on, the other is
[math]\displaystyle{ \nabla f = \left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right) }[/math]
For [math]\displaystyle{ n }[/math] variables we have a gradient with [math]\displaystyle{ n }[/math] coordinates. The flipped Delta is the letter Nabla, read it "del [math]\displaystyle{ f }[/math]".
We can rewrite the directional derivative using the gradient as follows
[math]\displaystyle{ \frac{\partial f}{\partial \overrightarrow{v}}(a,b) = \left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right) \cdot (a,b) = \nabla f \cdot \overrightarrow{v} }[/math]
The gradient is not a single vector, but a function that produces vectors (not points!) for given coordinates. A function always associates one or more inputs to just one point. The gradient associates two or more coordinates with a vector. We choose a certain point [math]\displaystyle{ (x,y, ..., n) }[/math] of the function's domain and the gradient produces a corresponding vector.
Note: with single variable functions we have the problem of finding the tangent line to a function's graph. With level curves we can find tangent lines too, but that's not the gradient! First, level curves aren't functions. Second, the gradient is perpendicular to the level curve because it expresses the rate of change from one level curve towards another. We first learn about derivatives in relationship with the tangent line, which may lead some people to think that the gradient is related to finding tangent lines to a level curve.
I'm going to explain a confusion between what is tangent and what is perpendicular for functions of two variables. The gradient has two coordinates. A level curve also has two coordinates. Both the gradient and the level curve are contained in the same plane. Only the function itself has depth, the third coordinate. The gradient cannot be perpendicular to the XY plane. The same plane that contains the function's domain. Think about a circular motion, there is always a vector that is tangent to the trajectory and another that is perpendicular, but both have two dimensions and are parallel to the same plane.
For three and more variables the gradient still retains the property of being perpendicular to level surfaces and beyond because the dot product is valid for vectors of [math]\displaystyle{ n }[/math] coordinates.
How to find the tangent line to a level curve? The answer for that is to look at level curves and think on the function of one variable that can, partially, trace it. For example, if the level curve is a circle, we can easily parametrize it. By doing that we find [math]\displaystyle{ x(t) }[/math] and [math]\displaystyle{ y(t) }[/math] and from there we can calculate derivatives of a single variable function.