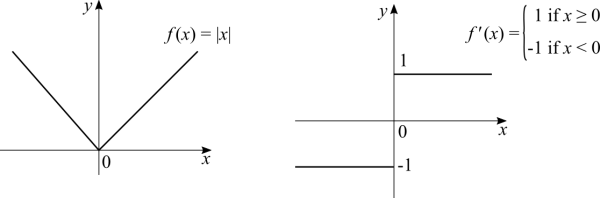
Conditions for differentiability for a single variable
For a function to be differentiable it has to be continuous. However, being continuous does not imply in differentiability. The graphical way to explain this is to show a function that is continuous but not smooth. The easiest example is [math]\displaystyle{ f(x) = |x| }[/math]. At the origin the function is continuous because the limit exists, but the derivative does not. It's rather counter-intuitive because the derivative is a limit, but not the same limit that we first learn. The other point that makes this counter-intuitive is the fact that we can trace a tangent line at the origin of [math]\displaystyle{ f(x) = |x| }[/math].
We didn't say that the previously mentioned function is not differentiable though. At the origin it isn't, but everywhere else it is differentiable. To put it in another words: every derivative is a limit that does exist; but not every limit is a derivative. If the limit doesn't exist at a point, then the derivative doesn't exist too at the same point. On the other hand, the existence of a limit at a point doesn't guarantee that the derivative also exists there. This is caused by the derivative being defined as a special case limit. Take the formal definition of a derivative and apply it using the idea of left and right limits to check it.
A natural question: we learn that a function can be discontinuous everywhere. Is there a function that is continuous everywhere, yet non differentiable everywhere? Yes, they exist and one example is the Weierstrass function. The function is continuous because if we take two points of it, there are never gaps in between them. The problem with differentiating it is that, although there aren't gaps in between two consecutive points, the rate of change abruptly changes everywhere. The graphical idea is to imagine a function that is continuous but has a sharp edge like the function above. Now imagine that every point of it is a sharp edge.
To simplify the concept let's say that a function is defined at a point [math]\displaystyle{ a }[/math]. Then for a 0.001 increment we have that [math]\displaystyle{ f(a + 0.001) }[/math] and [math]\displaystyle{ f(a - 0.001) }[/math] are almost the same value, with a distance that is close to zero. Weierstrass defined a function such that no matter if the distance between two consecutive points is small, the rate of change between [math]\displaystyle{ f(a + 0.001) }[/math] and [math]\displaystyle{ f(a - 0.001) }[/math] is significant to the point of making this function non-smooth everywhere. Another perspective: every process has some high frequency variations that we disregard when we model them with the common functions that everybody knows from school (assuming that you did learn them). The Weierstrass function is such that the high frequency variations are part of it and cannot be "smoothed out" in any way. We just can't "iron" this function as we do with clothes.
If you ever saw the graph of the stock market over time, in one day it's a rather unstable graph with high and low variations depending on the time of day. It's hard to define a derivative for it because it's rate of change is very unstable. The idea of a continuous and non-differentiable function is a function that represents some continuous process that has such high frequency variations that it's impossible to find the derivative at a given point. If one thinks about the motion of molecules, they are never "standing still" and are always vibrating. If we plot a graph representing Position x Time for a molecule, it intuitively is a continuous function, but at the same time it's graph is going to be full of spikes and jaggies. With computer graphics there is a performance measure that is frames per second. There is another unit that is milliseconds per frame or frametime. Due to the nature of computer graphics and specially if the program is interactive, the time it takes to render each frame can vary greatly, meaning that a function representing it is going to be hard to differentiate.
Prove that differentiability implies continuity
First we are assuming that the function is differentiable, which implies that the limit exists. Else, the theorem doesn't make sense. The assumption that the function is continuous is the same as [math]\displaystyle{ \lim_{x \ \to \ a} f(x) = f(a) }[/math]. Let's write the same but thinking on the tangent line:
[math]\displaystyle{ \frac{f(x) - f(a)}{x - a} - f'(a) = 0 }[/math]
[math]\displaystyle{ f(x) - f(a) - (x - a)f'(a) = 0 }[/math] (multiply everything by [math]\displaystyle{ x - a }[/math])
Now the tangent is equal to the derivative when we make the distance between the two equal to zero. For this to happen we calculate a limit when [math]\displaystyle{ x \to a }[/math]:
[math]\displaystyle{ \lim_{x \ \to \ a} [f(x) - f(a) - (x - a)f'(a)] = 0 }[/math]
[math]\displaystyle{ \lim_{x \ \to \ a} [f(x) - f(a)] = 0 }[/math]
[math]\displaystyle{ \lim_{x \ \to \ a} f(x) = f(a) }[/math]
([math]\displaystyle{ f(a) }[/math] does not depend on [math]\displaystyle{ x }[/math], that's why we can add it to both sides of the equation)
Note: for multivariable functions we have a similar concept using tangent planes.