Condições de diferenciabilidade para funções de uma variável
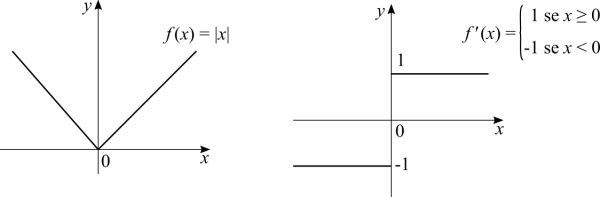
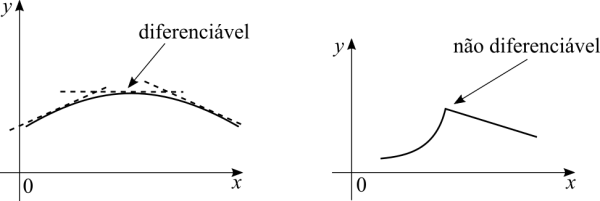
Para uma função ser diferenciável ela precisa ser contínua. Porém, continuidade não implica em diferenciabilidade. A maneira gráfica de explicar isto é mostrando uma função que seja contínua mas não suave. O exemplo mais fácil é [math]\displaystyle{ f(x) = |x| }[/math]. Na origem a função é contínua porque o limite existe, mas a derivada não. É bastante contra-intuitivo porque a derivada é um limite, mas não o mesmo limite que aprendemos num primeiro momento. O outro ponto que torna este fato contra-intuitivo é o fato que podemos traçar uma reta tangente na origem de [math]\displaystyle{ f(x) = |x| }[/math].
O que não foi dito é que a função mencionada anteriormente não era diferenciável. Na origem ela não é, mas em todos os outros pontos ela é. Em outras palavras: toda derivada é um limite que existe, mas nem todo limite é uma derivada. Se o limite não existir num ponto, então a derivada também não existe no mesmo ponto. Por outro lado, a existência do limite num ponto não garante a existência da derivada ali. Isto ocorre porque a derivada é definida como um caso especial de limite. Pegue a definição formal da derivada e aplique-a com a ideia de limites laterais para verificar.
Uma pergunta natural: aprendemos que uma função pode ser descontínua em todos os pontos. Existe uma função que seja contínua em todos os pontos e não diferenciável em nenhum deles ao mesmo tempo? Sim, existe e um exemplo é a Função de Weierstrass. A função é contínua porque se pegarmos dois pontos quaisquer, nunca existe um espaço vazio entre eles. O problema de diferenciar esta função é que, apesar dela ser contínua, a taxa de variação muda abruptamente em todos os pontos. A ideia gráfica é imaginar uma função que seja contínua mas pontiaguda como a função acima. Agora imagine que todos os pontos da função são serrilhados.
Para simplificar o conceito vamos supor que uma função esteja definida num ponto [math]\displaystyle{ a }[/math]. Depois, para um incremento de 0.001 temos que [math]\displaystyle{ f(a + 0.001) }[/math] e [math]\displaystyle{ f(a - 0.001) }[/math] são valores muito próximos, com uma distância quase nula. Weierstrass definiu uma função tal que, não importando quão pequena seja a distância entre dois pontos consecutivos, a taxa de variação entre [math]\displaystyle{ f(a + 0.001) }[/math] e [math]\displaystyle{ f(a - 0.001) }[/math] é significativa ao ponto de termos uma função que não é suave em lugar nenhum. Uma outra perspectiva: todo processo apresenta algumas variações de alta frequência que descartamos quando o modelamos com as funções mais conhecidas aprendidas na escola (assumindo que você aprendeu estas funções). A função de Weierstrass é tal que as variações de alta frequência são parte dela e é impossível "suavizá-la" de qualquer forma. Não temos como "passar um ferro" na função da mesma forma que fazemos com roupas.
Se você já viu o gráfico do mercado de ações sobre o tempo, num dia ele é um gráfico bastante instável com variações altas e baixas dependendo da hora do dia. É difícil de definir uma derivada para ele porque a sua taxa de variação é muito instável. A ideia de uma função contínua e não diferenciável é uma função que represente um processo contínuo que tenha tamanha alta frequência na sua variação que é impossível de achar uma derivada em algum ponto. Se você pensar no movimento de moléculas elas nunca ficam "paradas" e estão sempre vibrando. Se traçarmos um gráfico representando Posição x Tempo para uma molécula, intuitivamente o gráfico é contínuo, mas ao mesmo tempo será um gráfico cheio de picos e serrilhados. Com computação gráfico temos uma medida de desempenho que é quadros por segundo. Há uma outra que são os milissegundos por quadro ou tempo por quadro. Por causa da natureza da computação gráfica, em especial quando o programa é interativo, o tempo que é necessário para renderizar cada quadro varia enormemente. O que significa que uma função representando este tempo vai ser bem difícil de diferenciar.
Prove que diferenciabilidade implica em continuidade
Primeiro assumimos que a função é diferenciável, o que implica que o limite existe. Caso contrário o teorema não faz sentido. [math]\displaystyle{ \lim_{x \ \to \ a} f(x) = f(a) }[/math] é o mesmo que afirmar com palavras que uma função é contínua. Vamos escrever o mesmo mas pensando na reta tangente:
[math]\displaystyle{ \frac{f(x) - f(a)}{x - a} - f'(a) = 0 }[/math]
[math]\displaystyle{ f(x) - f(a) - (x - a)f'(a) = 0 }[/math] (multiplique tudo por [math]\displaystyle{ x - a }[/math])
Agora a tangente é igual à derivada quando reduzimos a distância entre as duas à zero. Para que isto aconteça calculamos o limite quando [math]\displaystyle{ x \to a }[/math]:
[math]\displaystyle{ \lim_{x \ \to \ a} [f(x) - f(a) - (x - a)f'(a)] = 0 }[/math]
[math]\displaystyle{ \lim_{x \ \to \ a} [f(x) - f(a)] = 0 }[/math]
[math]\displaystyle{ \lim_{x \ \to \ a} f(x) = f(a) }[/math]
([math]\displaystyle{ f(a) }[/math] não depende de [math]\displaystyle{ x }[/math]. É por isso que podemos adicioná-la a ambos os lados da equação)
Observação: para funções de várias variáveis temos um conceito similar com planos tangentes.