Graphs of the parabola, exp and log

To understand why a graph is a straight line or it's a curve you don't need to understand calculus, but you need to understand the tangent. This page here is meant to give a very rough idea of the graphs. I'm not going to talk about inflection points, critical points and derivatives here.

All you need to understand to plot one point of a function is to understand that each point is an ordered pair in the form [math]\displaystyle{ (x, \ f(x)) }[/math], with [math]\displaystyle{ f(x) }[/math] being the vertical axis.

In case you ask about the word "slope". I'm using slope, rate of change and tangent interchangeable here.

Depending on how hard it is to trace graphs by hand for you, heavily distorted graphs can very well lead to incorrect interpretation. I don't know if there are teachers who are pedantic with the "correctness" of graphs. In here I'd make a comment about straight lines x curves. Some people may find it hard to trace one or the other and it may be related to motor coordination or something. But there is also a matter of perfectionism where some people may tie the interpretation of some problems way too hard to the "correctness" of a graph.

The parabola

Have you ever asked yourself why is [math]\displaystyle{ f(x) = x^2 }[/math] a parabola? If [math]\displaystyle{ f(x) = x }[/math] is a straight line, how can the square be so different? I'm going to explain this with a pure geometrical reasoning.

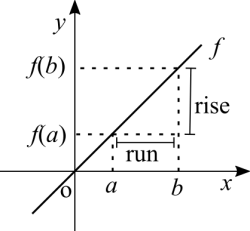
Look at the graph of [math]\displaystyle{ f(x) = x }[/math]. Every point of this function has this form [math]\displaystyle{ (x, y) }[/math] with [math]\displaystyle{ x = y }[/math]. Now the meaning of this equality in the graph is that for every step that you take in [math]\displaystyle{ x }[/math], the same step is taken in [math]\displaystyle{ f(x) }[/math]. In other words, one unit forwards is equal to one unit up and vice-versa. Take any two points where [math]\displaystyle{ b \gt a }[/math]. We have that [math]\displaystyle{ \frac{f(b) - f(a)}{b - a} = 1 }[/math]. See how the rise [math]\displaystyle{ f(b) - f(a) }[/math] and the run [math]\displaystyle{ b - a }[/math] are equal to each other? We have a name for the ratio rise / run and it's tangent. Do you remember from school that the tangent of 45° is 1? Right now you may be unaware of the definition of a derivative but we've just discussed the concept of the rate of change, which is the geometrical idea of a derivative.

Why is [math]\displaystyle{ f(x) = x }[/math] a straight line? Because its rate of change never changes! It's always constant and always equal to 1.

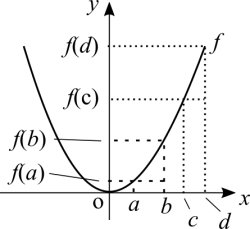
Now look at [math]\displaystyle{ f(x) = x^2 }[/math]. Take two points where [math]\displaystyle{ b \gt a }[/math]. For example: [math]\displaystyle{ f(1) = 1 }[/math] and [math]\displaystyle{ f(2) = 4 }[/math]. Now take another two points elsewhere, [math]\displaystyle{ f(3) = 9 }[/math] and [math]\displaystyle{ f(4) = 16 }[/math]. In the first case the rate of change is 1/3. In the second case the rate is 1/7. Every different pair of points that you choose is going to result in a different rate of change. This "proves" that the graph cannot be a straight line, because the rate of change between every pair of points is always different from the rate of another pair. For every step we take in [math]\displaystyle{ x }[/math], [math]\displaystyle{ f(x) }[/math] is going to be the square of the same distance. In other words, as we walk at a constant speed along the x axis, from 0 to infinity, each point of the graph is going higher and higher at even faster speeds. From 0 to negative infinity the same function's behaviour.

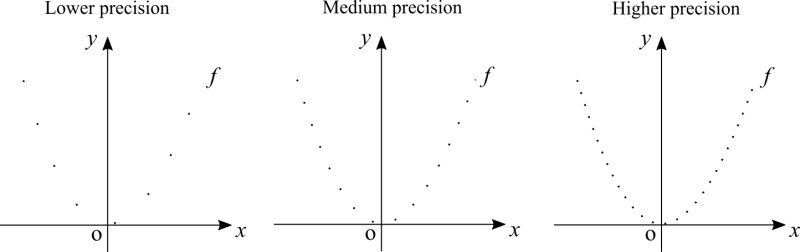
At school you may have learnt that the more points you plot, the more precise your graph is. How does a computer plot a graph? Back at school you may have had already noticed that when the points are very close to each other, connecting two points next to each other with a straight line did resemble a curve. That's how a computer plots a graph, it traces straight lines but because the points are so close to each other, we can't distinguish on screen a dot from a line. Right now you may be unaware of the definition of a limit, but to plot infinitely many points close to each other is the concept of a limit. Computers can't plot infinitely many points though because there isn't infinite time and because we don't need to. Also, screens with infinite resolution doesn't exist.

Now what happens with large, positive and even powers? It's a parabola, but we "flatten" it. The reason for this behaviour is quite simple. For [math]\displaystyle{ 0 \lt x \lt 1 }[/math] we have fractions and the denominator grows very large with very large powers. When [math]\displaystyle{ x \gt 1 }[/math] the power is so large that the function grows fast enough to become closer to a vertical line.

What about cubics and odd powers? The concept is the same of a parabola with just one difference. For [math]\displaystyle{ x \lt 0 }[/math] the graph goes down rather than up. Remember that the minus sign is kept with odd powers.

Note: In case you noticed that the above graph is slightly distorted compared to the real graph of a biquadratic function for example. I used inkscape to draw a bezier curve and because the software is unable to handle polynomials with a degree higher than cubics, the distortion that you are seeing is exactly the error associated in attempting to trace a biquadratic function using a cubic to approximate it. I've just explained in practical terms one of the fundamental problems that numerical methods have to solve, which is to approximate functions and minimize errors.

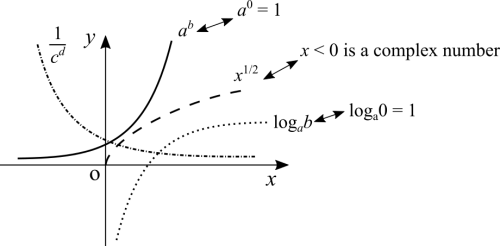
The exponential and logarithm

Take [math]\displaystyle{ a^b }[/math] with [math]\displaystyle{ a, \ b \gt 1 }[/math], for example [math]\displaystyle{ 2^2 }[/math]. You can easily notice that for every unit that you add to the power, the result is even larger. In other words, the rate of change is always changing and thus, the graph cannot be a straight line.

What happens if [math]\displaystyle{ 0 \lt a \lt 1 }[/math]? Then, if we keep increasing the power, it results in smaller and smaller numbers. It's an exponential that decreases for larger powers. The graph is not a straight line because the rate of change keeps changing as we move along it.

What happens if [math]\displaystyle{ a\gt 1 }[/math] and [math]\displaystyle{ 0 \lt b \lt 1 }[/math]? Then, from school, we have a root and the graphs of roots are also not a straight line.

The definition of a logarithm relies on the definition of the exponential. When we add the concept of functions we learn that the log and the exp are one the inverse function of the other.

Note: the same comment as above. I used bezier curves to trace the graphs of exponentials and logarithms. It's impossible for a polynomial to perfectly match the exp or log.