Gráficos da parábola, exp e log

Para entender poque um gráfico é uma linha reta ou uma curva você não precisa entender cálculo, mas você precisa entender a tangente. Esta página tem por objetivo dar uma ideia bastante superficial dos gráficos. Não vou discutir pontos de inflexão, pontos críticos ou derivadas aqui.

Tudo que você precisa entender para marcar um ponto de uma função no plano cartesiano é entender que cada ponto é um par ordenado da forma [math]\displaystyle{ (x, \ f(x)) }[/math], com [math]\displaystyle{ f(x) }[/math] sendo o eixo vertical.

Caso você pergunte sobre a palavra "inclinação". Aqui uso inclinação, tangente e taxa de variação como sinônimos.

Dependendo de quão difícil for traçar gráficos à mão para você, gráficos muito distorcidos podem muito bem levar à interpretações incorretas. Não sei se há professores muito pedantes quanto à "corretude" dos gráficos. Aqui eu comentaria sobre linhas retas x curvas. Algumas pessoas podem ter dificuldade com um ou outro e pode ter relação com a coordenação motora ou algo assim. Mas há também uma questão de perfeccionismo onde algumas pessoas podem se preocupar demasiadamente com a exatidão do gráfico, o que acaba interferindo com a interpretação do problema.

A parábola

Você já se perguntou por que [math]\displaystyle{ f(x) = x^2 }[/math] é uma parábola? Se [math]\displaystyle{ f(x) = x }[/math] é uma linha reta, como elevar ao quadrado muda tanto? Eu vou recorrer a um raciocínio puramente geométrico.

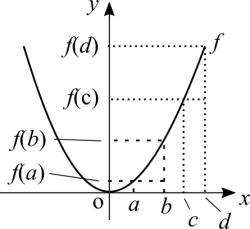
Olhe para o gráfico de [math]\displaystyle{ f(x) = x }[/math]. Cada ponto desta função tem a forma [math]\displaystyle{ (x, y) }[/math], onde [math]\displaystyle{ x = y }[/math]. Agora o significado gráfico desta equação é que para cada passo que você dá em [math]\displaystyle{ x }[/math], o mesmo passo é dado em [math]\displaystyle{ f(x) }[/math]. Em outras palavras, cada unidade para frente é igual a uma unidade para cima e vice-versa. Pegue dois pontos quaisquer com [math]\displaystyle{ b \gt a }[/math]. Temos que [math]\displaystyle{ \frac{f(b) - f(a)}{b - a} = 1 }[/math]. Vê como a altura [math]\displaystyle{ f(b) - f(a) }[/math] e o afastamento [math]\displaystyle{ b - a }[/math] são igual um ao outro? Nós temos um nome para a razão altura / afastamento e é tangente. Você se lembra da escola que a tangente de 45° é 1? Até aqui você pode não saber a definição de uma derivada, mas acabamos de discutir o conceito de taxa de variação, que é a ideia geométrica da derivada.

Por quê [math]\displaystyle{ f(x) = x }[/math] é uma linha reta? Porque a sua taxa de variação nunca muda! Sempre é constante e igual a 1.

Agora veja [math]\displaystyle{ f(x) = x^2 }[/math]. Pegue dois pontos onde [math]\displaystyle{ b \gt a }[/math]. Por exemplo: [math]\displaystyle{ f(1) = 1 }[/math] e [math]\displaystyle{ f(2) = 4 }[/math]. Agora escolha dois pontos diferentes dos anteriores, por exemplo [math]\displaystyle{ f(3) = 9 }[/math] e [math]\displaystyle{ f(4) = 16 }[/math]. No primeiro caso a taxa de variação é 1/3. No segundo caso é 1/7. Cada par de pontos que você escolher vai resultar numa taxa de variação diferente. Isto "prova" que o gráfico não pode ser uma linha reta, porque a taxa de variação para cada par de pontos sempre difere da taxa de outro par. Para cada passo que dermos em [math]\displaystyle{ x }[/math], [math]\displaystyle{ f(x) }[/math] é o quadrado da mesma distância. Em outras palavras, enquanto caminhamos numa taxa constante no eixo x, do zero até infinito, cada ponto do gráfico esta subindo cada vez mais alto. Do zero para o lado negativo do eixo o mesmo comportamento da função é observado no gráfico.

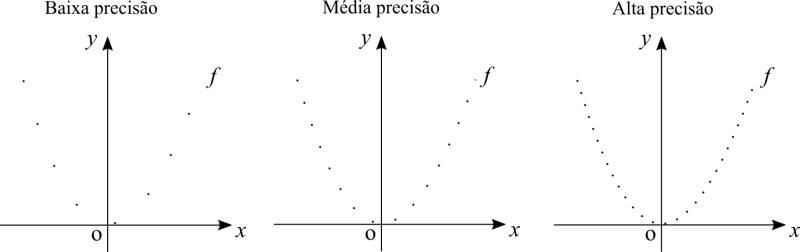
Na escola provavelmente você aprendeu que quanto mais pontos você marca, mais preciso fica o gráfico. Como um computador desenha um gráfico? Lá na escola você já deve ter percebido que quanto mais pontos próximos uns dos outros, ligando-os com uma linha reta, o desenho se aproxima de uma curva (a menos que os pontos em si estejam alinhados numa linha reta). É assim que um computador traça um gráfico, ligando pontos com linhas retas. Mas como os pontos estão muito próximos uns dos outros não conseguimos mais distinguir um ponto de uma linha. Até aqui você pode não saber a definição de um limite, mas o processo de marcar infinitos pontos um perto do outro é o conceito de limite. Porém um computador não pode marcar infinitos pontos porque não há tempo infinito e também não é preciso. Além das telas não terem uma resolução infinita.

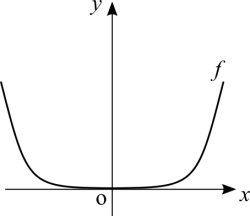
Agora o que acontece com potências grandes, positivas e pares? É uma parábola, mas a base fica "achatada". A razão para este comportamento é bastante simples. Para [math]\displaystyle{ 0 \lt x \lt 1 }[/math] temos frações e o denominador cresce muito para números grandes. Quando [math]\displaystyle{ x \gt 1 }[/math] a potência é tão alta que a função cresce muito rapidamente e se aproxima de uma reta vertical.

E quanto a potências ímpares e cubos? O conceito é o mesmo de uma parábola com uma pequena diferença. Para [math]\displaystyle{ x \lt 0 }[/math] o gráfico vai para negativo ao invés de positivo. Lembre-se que o sinal de menos se mantém com potências ímpares.

Observação: Caso você tenha notado que o gráfico acima é um pouco distorcido em relação ao gráfico real de uma função biquadrada por exemplo. Eu usei o inkscape para traçar uma curva de Bezier e como o software só lida com curvas polinomiais de grau 3, a distorção que você vê é exatamente o erro associado na aproximação que eu fiz do gráfico. Eu acabei de explicar em termos práticos um dos problemas fundamentais dos métodos numéricos, que é aproximar uma função por outra, enquanto se tenta minimizar o erro ou as diferenças.

A exponencial e o logaritmo

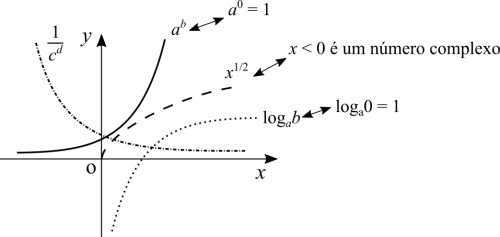
Pegue [math]\displaystyle{ a^b }[/math] com [math]\displaystyle{ a, \ b \gt 1 }[/math]. Por exemplo [math]\displaystyle{ 2^2 }[/math]. Você pode facilmente notar que para cada unidade que você aumenta na potência, o resultado é ainda maior. Em outras palavras, a taxa de variação sempre muda e portanto, o gráfico não pode ser uma linha reta.

O que acontece se [math]\displaystyle{ 0 \lt a \lt 1 }[/math]? Se continuarmos a aumentar a potência, o resultado é um número cada vez menor. É uma exponencial que decresce para potências grandes. O gráfico não é uma linha reta porque a taxa de variação muda a cada passo que se dá.

O que acontece no caso [math]\displaystyle{ a \gt 1 }[/math] e [math]\displaystyle{ 0 \lt b \lt 1 }[/math]? Na escola aprendemos que potências racionais são raízes e a taxa de variação também não será constante.

A definição do logaritmo depende da definição da exponencial. Quando adicionamos o conceito de função, aprendemos que o log e a exp são uma a função inversa da outra.

Observação: o mesmo comentário de cima. Eu usei curvas de Bezier para traçar o gráfico das exponenciais e logaritmos. É impossível uma curva descrita por um polinômio de grau 3 traçar peritamente o log ou exp.